Question

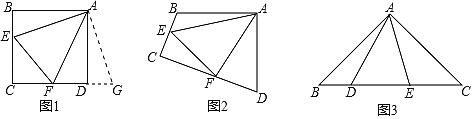
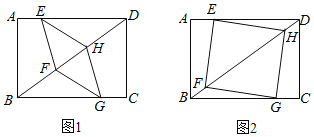
【题目】矩形ABCD，AB=6，BC=8，四边形EFGH的顶点E、G在矩形的边AD、BC上；顶点F、H在矩形的对角线BD上．

（1）如图1，当四边形EFGH是平行四边形时，求证：△DEH≌△BGF．

（2）如图2，当四边形EFGH是正方形时，求BF的长．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）由EH=FG，∠BFG=∠EHD，∠EDH=∠GBF，即可证明；

（2）证明△HKG≌△GMF（AAS），利用BC=BM+MG+GK+KC=8，即可求解．

解：在Rt△BCD中，tan∠DBC=

=tanα，则sin，cosα=，

∵四边形ABCD为矩形，

∴AD∥BC，

∴∠EDH=∠GBF，

（1）∵四边形EFGH是平行四边形，

∴EH=FG，∠EHF=∠GFH，

∴∠BFG=180°﹣∠GFH，∠EHD=180°﹣∠EHF=∠BFG，

又∵∠EDH=∠GBF，

∴△DEH≌△BGF（AAS）；

（2）∵四边形EFGH是正方形也为平行四边形，

故由（1）得：△DEH≌△BGF（AAS），

∴BF=DH，

设BF=x=DH，

如下图，过点H作HK⊥BC于点K，作HN⊥CD于点N，作FM⊥BC于点M，

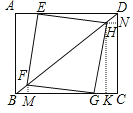
在Rt△BFM中，FM=BFsin∠FBM=xsinα==DN，

同理BM==HN=CK，

∵∠FGM+∠HGK=90°，∠HGK+∠GHK=90°，

∴∠GHK=∠FGM，

又∵∠HKG=∠GMF=90°，FG=GH，

∴△HKG≌△GMF（AAS），

∴GM=HK=CN=CD﹣DN=6﹣，GK=FM=，

∴BC=BM+MG+GK+KC=+（6﹣）+=8，

解得：x=，

即BF的长为．