题目内容
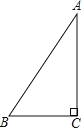
【题目】如图，已知Rt△ABC中∠C=90°，AB=10，AC=8．
（1）作AB的垂直平分线DE，交AB于点D，交AC于点E．(要求尺规作图，不写作法，保留作图痕迹)；
（2）求AE的长．
【答案】（1）作图见解析；（2）AE=
．
【解析】
（1）依据线段的垂直平分线的判定进行作图，即可得到AB的垂直平分线DE；
（2）连接BE，设AE=x，则BE=x，CE=8-x，依据勾股定理可得：在Rt△BCE中，
，解方程即可得到AE的长.
（1）如图所示，分别以
为圆心，大于
为半径画弧，两弧交于
，作直线
交
于D，交
于E，则DE即为所求；
（2）如图，连接BE．
∵DE垂直平分AB，
∴AE=BE，
设AE=x，则BE=x，CE=8﹣x．
∵Rt△ABC中∠C=90°，AB=10，AC=8，
∴BC=6．
∵Rt△BCE中，BC2+CE2=BE2，
∴62+(8﹣x)2=x2，
解得：
∴
练习册系列答案
相关题目
