题目内容
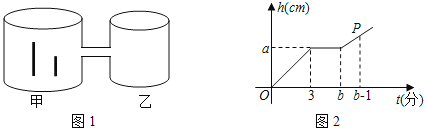
【题目】如图1是两圆柱形连通容器,两根铁棒直立于甲容器底部(连通处及铁棒体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)与时间t(分)的函数关系如图2所示.已知两根铁棒的长度之和为34cm,当水面达到连通处时,一根露出水面的长度是它的![]() ,另一根露出水面的长度是它的
,另一根露出水面的长度是它的![]() .
.
(1)①图2中(3,a)表示的实际意义是 ;
②请求出a的值;
(2)若甲、乙两容器的底面积之比为S甲,S乙=3:2.
①直接写出b的值为 ;
②求点P的坐标.
【答案】(1)①注水3分钟后甲容器的水面高度达到联通处;②a=12;(2)①5;②(6,![]() ).
).
【解析】
(1)①根据图示表示的意义解答即可;②根据题意列出方程解答即可;
(2)①根据图示得出B的值即可;②根据题意得出比例关系解答即可.
解:(1)①(3,a)表示的实际意义是注水3分钟后甲容器的水面高度达到联通处;
②由题意,两根铁棒长度分别为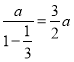 ,
,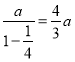 ,
,
可得:![]() ,
,
解得:a=12,
(2)①b=5;
②由题意b+1=6,5分钟时甲乙容器的水面高度都达到联通处,此时水面高为12,
设S甲=3k,S乙=2k,则每分钟注水体积![]() ,
,
∴6分钟时水面高为![]() ,
,
∴即点P的坐标为(6,![]() ).
).
故答案为:注水3分钟后甲容器的水面高度达到联通处;5.

【题目】小明去超市采购防疫物品,超市提供下表所示![]() 、
、![]() 两种套餐,小明决定购买50份
两种套餐,小明决定购买50份![]() 套餐.超市为了促进消费,给出两种优惠方式,方式一:现金支付总额每满700元立减200元;方式二:现金支付总额每满600元送300元现金券,现金券可等同现金使用,但是使用现金券的总额不能超过应付总金额.
套餐.超市为了促进消费,给出两种优惠方式,方式一:现金支付总额每满700元立减200元;方式二:现金支付总额每满600元送300元现金券,现金券可等同现金使用,但是使用现金券的总额不能超过应付总金额.
套餐类别 | 一次性防护口罩 | 免洗洗手液 | 套餐价格 |
| 2包 | 1瓶 | 71元 |
| 1包 | 2瓶 | 67元 |
(1)求一次性防护口罩和免洗洗手液各自的单价;
(2)小明觉得优惠方式二比方式一的优惠力度更大,他计划分两次购买,第一次付现金购买一部分![]() 套餐,获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱?
套餐,获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱?