Question

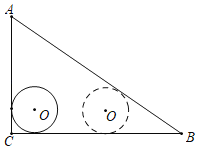
【题目】如图，Rt△ACB中，∠C=90°，AC=6，BC=8，半径为1的⊙O与AC，BC相切，当⊙O沿边CB平移至与AB相切时，则⊙O平移的距离为（　　）

A.3B.4C.5D.6

Answer 1

【答案】B

【解析】

设⊙O与AC相切于D，与BC相切于H，平移后的⊙O′与AB相切于F，与BC相切于E，连接OH，O′D，则点O在O′D上，连接O′F，EO′并延长交AB于G，根据正方形和矩形的性质得到OD=OH=O′E=O′F=CD=CH=1，OO′=HE，根据相似三角形的判定和性质定理即可得到结论．

解：∵Rt△ACB中，∠C=90°，AC=6，BC=8，

∴AB=10，

设⊙O与AC相切于D，与BC相切于H，平移后的⊙O′与AB相切于F，与BC相切于E，

连接OH，O′D，则点O在O′D上，连接O′F，EO′并延长交AB于G，

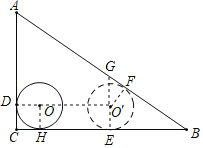
∴四边形CDOH是正方形，四边形OHEO′是矩形，

∴OD=OH=O′E=O′F=CD=CH=1，OO′=HE，

∴EG⊥BC，

∵∠C=90°，

∴EG∥AC，

∴∠FGE=∠A，

∵∠GFO′=∠C=90°，

∴∠O′FG∽∠BCA，

∴，

∴，

∴O′G=，

∴EG=，

∵GE∥AC，

∴△BGE∽△BAC，

∴，

∴，

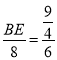∴BE=3，

∴OO′=HE=BC﹣CH﹣BE=8﹣1﹣3=4，

∴⊙O平移的距离为4，

故选：B．