Question

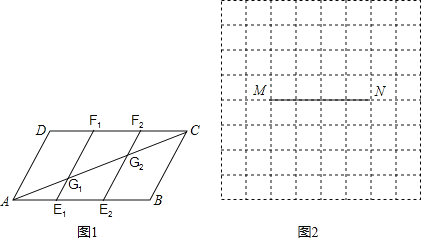
【题目】(1)如图1，在平行四边形ABCD中，点E1，E2是AB三等分点，点F1，F2是CD三等分点，E1F1，E2F2分别交AC于点G1，G2，求证：AG1＝G1G2＝G2C．

(2)如图2，由64个边长为1的小正方形组成的一个网格图，线段MN的两个端点在格点上，请用一把无刻度的尺子，画出线段MN三等分点P，Q．(保留作图痕迹)

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

(1)利用平行线分线段成比例定理证明即可．

(2)利用(1)中结论，构造平行四边形解决问题即可．

解：

(1)证明：如图1中，

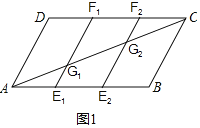
∵四边形ABCD是平行四边形，

∴AB＝CD，AB∥CD，AD∥BC，

∵DF1＝CD，AE1＝AB，

∴DF1＝AE1，

∴四边形ADF1E1是平行四边形，

∴AD∥E1F1，

∴E1G1∥BC，

∴，

同法可证：，

∴AG1＝CG2＝AC，

∴AG1＝G1G2＝G2C．

(2)如图，点P，Q即为所求．