ÌâÄżÄÚÈĘ
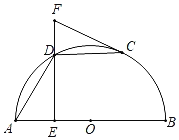
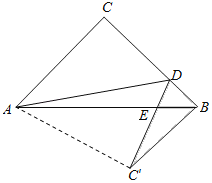
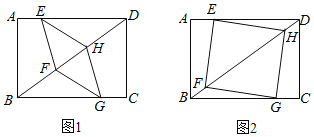
ĄŸÌâÄżĄżÌœŸżŁșÈçÍŒ1șÍÍŒ2ŁŹËıßĐÎABCDÖĐŁŹÒŃÖȘABŁœADŁŹĄÏBADŁœ90ĄăŁŹ”ăEĄąF·Ö±đÔÚBCĄąCDÉÏŁŹĄÏEAFŁœ45ĄăŁź
Łš1Ł©ąÙÈçÍŒ1ŁŹÈôĄÏBĄąĄÏADC¶ŒÊÇÖ±œÇŁŹ°ŃĄśABEÈÆ”ăAÄæʱŐëĐęŚȘ90ĄăÖÁĄśADGŁŹÊčABÓëADÖŰșÏŁŹÖ±œÓĐŽłöÏ߶ÎBEĄąDFșÍEFÖźŒä”ÄÊęÁżčŰÏ”ĄĄ ĄĄŁ»
ąÚÈçÍŒ2ŁŹÈôĄÏBĄąĄÏD¶ŒČ»ÊÇÖ±œÇŁŹ”«ÂúŚăĄÏB+ĄÏDŁœ180ĄăŁŹÏ߶ÎBEĄąDFșÍEFÖźŒä”ÄœáÂÛÊÇ·ńÈÔÈ»łÉÁąŁŹÈôłÉÁąŁŹÇëĐŽłöրÜčęłÌŁ»ÈôČ»łÉÁąŁŹÇë˔ÜÀíÓÉŁź
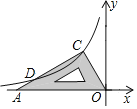
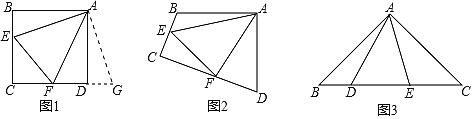
Łš2Ł©ÍŰŐčŁșÈçÍŒ3ŁŹÔÚĄśABCÖĐŁŹĄÏBACŁœ90ĄăŁŹABŁœACŁœ2![]() Łź”ăDĄąEŸùÔÚ±ßBC±ßÉÏŁŹÇÒĄÏDAEŁœ45ĄăŁŹÈôBDŁœ1ŁŹÇóDE”Äł€Łź
Łź”ăDĄąEŸùÔÚ±ßBC±ßÉÏŁŹÇÒĄÏDAEŁœ45ĄăŁŹÈôBDŁœ1ŁŹÇóDE”Äł€Łź
ĄŸŽđ°žĄżŁš1Ł©ąÙEFŁœBE+DFŁ»ąÚłÉÁąŁŹÀíÓÉÏêŒûœâÎöŁ»Łš2Ł©DEŁœ![]() Łź
Łź
ĄŸœâÎöĄż
Łš1Ł©ąÙžùŸĘĐęŚȘ”ÄĐÔÖÊ”ĂłöAEŁœAGŁŹĄÏBAEŁœĄÏDAGŁŹBEŁœDGŁŹÇółöĄÏEAFŁœĄÏGAFŁœ45ĄăŁŹžùŸĘSASÍÆłöĄśEAFĄŐĄśGAFŁŹžùŸĘÈ«”ÈÈęœÇĐΔÄĐÔÖÊ”ĂłöEFŁœGFŁŹŒŽżÉÇółöŽđ°žŁ»
ąÚžùŸĘĐęŚȘ”ÄĐÔÖÊŚśžšÖúÏߣŹ”ĂłöAEŁœAGŁŹĄÏBŁœĄÏADGŁŹĄÏBAEŁœĄÏDAGŁŹÇółöCĄąDĄąGÔÚÒ»ÌőÖ±ÏßÉÏŁŹžùŸĘSASÍÆłöĄśEAFĄŐĄśGAFŁŹžùŸĘÈ«”ÈÈęœÇĐΔÄĐÔÖÊ”ĂłöEFŁœGFŁŹŒŽżÉÇółöŽđ°žŁ»
Łš2Ł©ÈçÍŒ3ŁŹÍŹÀ팜ĐęŚȘÈęœÇĐÎŁŹžùŸĘ”ÈŃüÖ±œÇÈęœÇĐÎĐÔÖÊșÍčŽčɶšÀíÇółöĄÏABCŁœĄÏCŁœ45ĄăŁŹBCŁœ4ŁŹžùŸĘĐęŚȘ”ÄĐÔÖÊ”ĂłöAFŁœAEŁŹĄÏFBAŁœĄÏCŁœ45ĄăŁŹĄÏBAFŁœĄÏCAEŁŹÇółöĄÏFADŁœĄÏDAEŁœ45ĄăŁŹÖ€ĄśFADĄŐĄśEADŁŹžùŸĘÈ«”È”ĂłöDFŁœDEŁŹÉèDEŁœxŁŹÔòDFŁœxŁŹBFŁœCEŁœ3©xŁŹžùŸĘčŽčɶšÀí”Ăłö·œłÌŁŹÇółöxŒŽżÉŁź
œâŁșŁš1Ł©Ąß°ŃĄśABEÈÆ”ăAÄæʱŐëĐęŚȘ90ĄăÖÁĄśADGŁŹÊčABÓëADÖŰșÏŁŹ
ĄàAEŁœAGŁŹĄÏBAEŁœĄÏDAGŁŹBEŁœDGŁŹĄÏBŁœĄÏADGŁœ90ĄăŁŹ
ĄßĄÏADCŁœ90ĄăŁŹ
ĄàĄÏADC+ĄÏADGŁœ90Ąă
ĄàFĄąDĄąGčČÏߣŹ
ĄßĄÏBADŁœ90ĄăŁŹĄÏEAFŁœ45ĄăŁŹ
ĄàĄÏBAE+ĄÏDAFŁœ45ĄăŁŹ
ĄàĄÏDAG+ĄÏDAFŁœ45ĄăŁŹ
ŒŽĄÏEAFŁœĄÏGAFŁœ45ĄăŁŹ
ÔÚĄśEAFșÍĄśGAFÖĐŁŹ
Ąß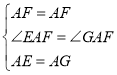 ŁŹ
ŁŹ
ĄàĄśEAFĄŐĄśGAFŁšSASŁ©ŁŹ
ĄàEFŁœGFŁŹ
ĄßBEŁœDGŁŹ
ĄàEFŁœGFŁœDF+DGŁœBE+DFŁŹ
čÊŽđ°žÎȘŁșEFŁœBE+DFŁ»
ąÚłÉÁąŁŹ
ÀíÓÉŁșÈçÍŒ2ŁŹ°ŃĄśABEÈÆA”ăĐęŚȘ”œĄśADGŁŹÊčABșÍADÖŰșÏŁŹ

ÔòAEŁœAGŁŹĄÏBŁœĄÏADGŁŹĄÏBAEŁœĄÏDAGŁŹ
ĄßĄÏB+ĄÏADCŁœ180ĄăŁŹ
ĄàĄÏADC+ĄÏADGŁœ180ĄăŁŹ
ĄàCĄąDĄąGÔÚÒ»ÌőÖ±ÏßÉÏŁŹ
ÓëąÙÍŹÀí”ĂŁŹĄÏEAFŁœĄÏGAFŁœ45ĄăŁŹ
ÔÚĄśEAFșÍĄśGAFÖĐŁŹ
Ąß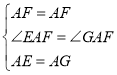 ŁŹ
ŁŹ
ĄàĄśEAFĄŐĄśGAFŁšSASŁ©ŁŹ
ĄàEFŁœGFŁŹ
ĄßBEŁœDGŁŹ
ĄàEFŁœGFŁœBE+DFŁ»
Łš2Ł©œâŁșĄßĄśABCÖĐŁŹABŁœACŁœ2![]() ŁŹĄÏBACŁœ90ĄăŁŹ
ŁŹĄÏBACŁœ90ĄăŁŹ
ĄàĄÏABCŁœĄÏCŁœ45ĄăŁŹ
ÓÉčŽčɶšÀí”ĂŁșBCŁœ![]() Łœ4ŁŹ
Łœ4ŁŹ
ÈçÍŒ3ŁŹ°ŃĄśAECÈÆA”ăĐęŚȘ”œĄśAFBŁŹÊčABșÍACÖŰșÏŁŹÁŹœÓDFŁŹ
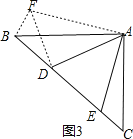
ÔòAFŁœAEŁŹĄÏFBAŁœĄÏCŁœ45ĄăŁŹĄÏBAFŁœĄÏCAEŁŹ
ĄßĄÏDAEŁœ45ĄăŁŹ
ĄàĄÏFADŁœĄÏFAB+ĄÏBADŁœĄÏCAE+ĄÏBADŁœĄÏBAC©ĄÏDAEŁœ90Ąă©45ĄăŁœ45ĄăŁŹ
ĄàĄÏFADŁœĄÏDAEŁœ45ĄăŁŹ
ÔÚĄśFADșÍĄśEADÖĐ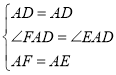 ŁŹ
ŁŹ
ĄàĄśFADĄŐĄśEADŁšSASŁ©ŁŹ
ĄàDFŁœDEŁŹ
ÉèDEŁœxŁŹÔòDFŁœxŁŹ
ĄßBCŁœ4ŁŹ
ĄàBFŁœCEŁœ4©1©xŁœ3©xŁŹ
ĄßĄÏFBAŁœ45ĄăŁŹĄÏABCŁœ45ĄăŁŹ
ĄàĄÏFBDŁœ90ĄăŁŹ
ÓÉčŽčɶšÀí”ĂŁșDF2ŁœBF2+BD2ŁŹ
x2ŁœŁš3©xŁ©2+12ŁŹ
œâ”ĂŁșxŁœ![]() ŁŹ
ŁŹ
ŒŽDEŁœ![]() Łź
Łź

 ÌìÌìÏòÉÏÒ»±ŸșĂŸíÏ”ÁĐŽđ°ž
ÌìÌìÏòÉÏÒ»±ŸșĂŸíÏ”ÁĐŽđ°ž ХѧÉú10·ÖÖÓÓŠÓĂÌâÏ”ÁĐŽđ°ž
ХѧÉú10·ÖÖÓÓŠÓĂÌâÏ”ÁĐŽđ°ž