Question

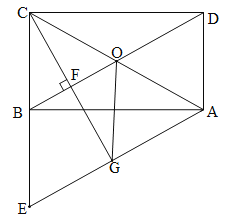
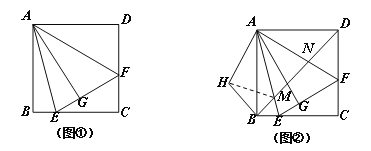
【题目】如图①，在正方形ABCD中，△AEF的顶点E，F分别在BC，CD边上，高AG与正方形的边长相等，

（1）求∠EAF的度数；

（2）在图①中，连结BD分别交AE、AF于点M、N，将△ADN绕点A顺时针旋转90°至△ABH位置，连结MH，得到图②．求证：MN2＝MB2＋ ND2 ；

（3）在图②中，若AG＝12， BM＝，直接写出MN的值．

Answer 1

【答案】（1）45°；（2）证明见解析；（3）.

【解析】（1）∵正方形ABCD，AG⊥EF，

∴AG＝AB，∠ABE＝∠AGE＝∠BAD＝90°，AE＝AE，

∴Rt△ABE≌Rt△AGE，∴∠BAE＝∠GAE，……………………………………2分

同理Rt△ADF≌Rt△AGF，∴∠GAF＝∠DAF，…………………………………4分

∴∠EAF＝∠BAD＝45°；…………………………………………………………5分

（2）证明：由旋转知，∠BAH=∠DAN，AH=AN，……………………………………7分

∵∠BAD=90°，∠EAF=45°，∴∠BAM+∠DAN=45°，

∴∠HAM=∠BAM+∠BAH=∠BAM+∠DAN =45°，

∴∠HAM=∠NAM，AM=AM，

∴△AHM≌△ANM，…………………………………………………………………8分

∴MN=MH，∵四边形ABCD是正方形，∴∠ADB=∠ABD=45°

由旋转知，∠ABH=∠ADB=45°，HB=ND，

∴∠HBM=∠ABH+∠ABD=90°，……………………………………………………9分

∴，∴；…………………………………10分

（3）.…………………………………………………………………………………12分

以下解法供参考∵，∴；

在（2）中，

设，则．

∴．即.