题目内容
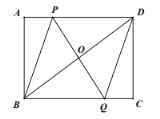
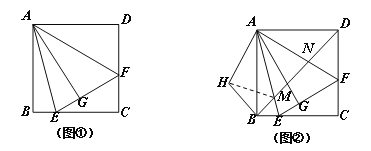
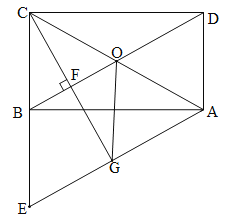
【题目】如图，在矩形
中，
、
相交于点
，过点
作的平行线
交
的延长线于点
．
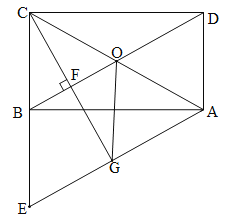
（1）求证：
．
（2）过点
作
于点
，并延长
交于点
，连接
．若
，
，求四边形
的周长．
【答案】（1）证明见解析；（2）
．
【解析】
（1）根据两组对边分别平行且的四边形是平行四边形判断出四边形BEAD是平行四边形，再根据平行四边形对边相等和矩形对边相等即可得出结论；
（2）根据矩形的对角线相等且互相平分及直角三角形斜边上的中线等于斜边的一半可得OB=OC=OG，利用勾股定理求出BC，CO的长．证明BF为△CEG的中位线，再由三角形中位线定理可得EG=2BF，最后根据四边形的周长公式列式计算即可得解．
（1）∵AE∥DB，AD∥EB，∴四边形BEAD是平行四边形，∴BE=DA．
∵四边形ABCD是矩形，∴BC=AD，∴BE=BC；
（2）∵四边形ABCD是矩形，∴OA=OB=OC
AC．
∵AE∥DB，CF⊥BO，∴CG⊥AE，∴GO为Rt△CGA斜边的中线，∴GOAC=OB，∴BO+OG=BD．
∵CF=6，BF=3，∴BE=BC=
．
设CO=x，则FO=BO-BF=x-3．在Rt△CFO中，∵
，∴
，解得：x=7.5，∴BO+OG=BD=2x=15．
∵OG=CO，OF⊥CG，∴FG=CF=6．
∵CB=BE，∴BF为△CEG的中位线，∴EG=2BF=6，∴四边形BOGE的周长=BO+OG+EG+EB=15+6+
=．
【题目】某篮球队对队员进行定点投篮测试，每人每天投篮10次，现对甲、乙两名队员在五天中进球数（单位：个）进行统计，结果如下：
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算，甲进球的平均数为8，方差为3.2.
（1）求乙进球的平均数和方差；
（2）如果综合考虑平均成绩和成绩稳定性两方面的因素，从甲、乙两名队员中选出一人去参加定点投篮比赛，应选谁？为什么？
【题目】学校组织八年级350名学生参加“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分，为了更好地了解本次大赛的成绩分布情况，随机抽取了其中若干名学生的成绩作为样本进行整理，得到下列不完整的统计图表：
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
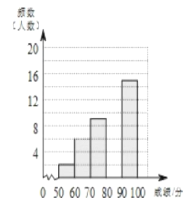
请根据所给信息，解答下列问题：
（1）求a和b的值；
（2）请补全频数分布直方图。
【题目】一种商品按销售量分三部分制定销售单价，如下表：
销售量 | 单价 |
不超过100件的部分 | 2.8元/件 |
超过100件不超过300件的部分 | 2.2元/件 |
超过300件的部分 | 2元/件 |
（1）若买100件花 元，买300件花 元；买380件花 元；
（2）小明买这种商品花了500元，求购买了这种商品多少件；
（3）若小明花了n元（n>280），恰好购买0.4n件这种商品，求n的值．
