��Ŀ����
����Ŀ��ij�������ۼס���������ë����֪������ë��ÿͲ���ۼ۱�������ë���15Ԫ������ʦ�Ӹ����깺����2Ͳ������ë���3Ͳ������ë������255Ԫ��
��1��������ס���������ë��ÿͲ���ۼ۸��Ƕ���Ԫ��
��2������������������������ò�����8780Ԫ�����ס���������ë��200Ͳ���Ҽ�����ë�����������������ë��������![]() ����֪������ë��ÿͲ�Ľ���Ϊ50Ԫ��������ë��ÿͲ�Ľ���Ϊ40Ԫ��
����֪������ë��ÿͲ�Ľ���Ϊ50Ԫ��������ë��ÿͲ�Ľ���Ϊ40Ԫ��
�����蹺��������ë��mͲ������������ļ��ֽ���������
������������ë�����ȫ���۳��������������������W��Ԫ���������ë�������m��Ͳ��֮��ĺ�����ϵʽ����˵����mΪ��ֵʱ�������������������Ƕ��٣�
���𰸡���1�������������ë��ÿͲ���ۼ�Ϊ60Ԫ��������ë��ÿͲ���ۼ�Ϊ45Ԫ����2���ٽ���������3�֣�������������ڵ�m=78ʱ��������������������Ϊ1390Ԫ��
����������1���������ë��ÿͲ���ۼ�ΪxԪ��������ë��ÿͲ���ۼ�ΪyԪ�����������з����飬�����ô𰸣�
��2�����蹺��������ë��mͲ����������ë��Ϊ��200��m��Ͳ���������ɵõ�����m�IJ���ʽ�飬������m��ȡֵ��Χ����mΪ������������m��ֵ��������ý���������
����m�ɱ�ʾ��W���ɵõ�����m��һ�κ���������һ�κ��������ʿ���ô𰸣�
��1���������ë��ÿͲ���ۼ�ΪxԪ��������ë��ÿͲ���ۼ�ΪyԪ��
��������ɵ�![]() �����
�����![]() ��
��
�𣺸����������ë��ÿͲ���ۼ�Ϊ60Ԫ��������ë��ÿͲ���ۼ�Ϊ45Ԫ��
��2����������������ë��mͲ����������ë��Ϊ��200��m��Ͳ��
��������ɵ�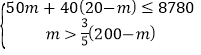 �����75��m��78��
�����75��m��78��
��m������
��m��ֵΪ76��77��78��
�����������3�֣��ֱ�Ϊ��
����һ������������ë��76Ͳ��������ë��Ϊ124Ͳ��
������������������ë��77Ͳ��������ë��Ϊ123Ͳ��
����һ������������ë��78Ͳ��������ë��Ϊ122Ͳ��
�ڸ�������ɵ�W=��60��50��m+��45��40����200��m��=5m+1000��
��5��0��
��W��m�������������75��m��78��
�൱m=78ʱ��W���W���ֵΪ1390��
�𣺵�m=78ʱ��������������������Ϊ1390Ԫ��

 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д�