Question

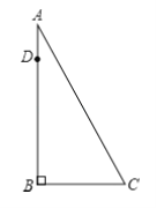
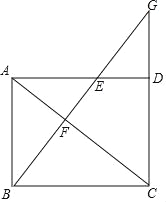
【题目】已知：如图，在平行四边形ABCD中，AC为对角线，E是边AD上一点，BE⊥AC交AC于点F，BE、CD的延长线交于点G，且∠ABE＝∠CAD．

（1）求证：四边形ABCD是矩形；

（2）如果AE＝EG，求证：AC2＝BCBG．

Answer 1

【答案】(1)见解析;(2)见解析.

【解析】

(1)、因为四边形ABCD是平行四边形，所以只要证明∠BAD=90°，即可得到四边形ABCD是矩形；(2)、连接AG，由平行四边形的性质和矩形的性质以及结合已知条件可证明△BCG∽△ABC，再由相似三角形的性质：对应边的比值相等即可证明AC2=BCBG．

(1)、解：证明： ∵BE⊥AC， ∴∠AFB=90°．

∴∠ABE+∠BAF=90°． ∵∠ABE=∠CAD． ∴∠CAD+∠BAF=90°． 即∠BAD=90°．

∵四边形ABCD是平行四边形， ∴四边形ABCD是矩形；

(2)、解：连接AG． ∵AE=EG， ∴∠EAG=∠EGA， ∵四边形ABCD是平行四边形，

∴AB∥CD，AD∥BC， ∴∠ABG=∠BGC， ∴∠CAD=∠BGC， ∴∠AGC=∠GAC，

∴CA=CG， ∵AD∥BC， ∴∠CAD=∠ACB， ∴∠ACB=∠BGC，

∵四边形ABCD是矩形， ∴∠BCG=90°， ∴∠BCG=∠ABC， ∴△BCG∽△ABC，

∴ ， ∴AC2=BCBG．