题目内容
【题目】已知反比例函数![]() (k为常数,k≠1).
(k为常数,k≠1).
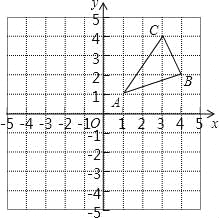
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
【答案】(Ⅰ)5(Ⅱ)k>1(Ⅲ)x1>x2
【解析】解:(Ⅰ)由题意,设点P的坐标为(m,2)
∵点P在正比例函数y=x的图象上,∴2=m,即m=2。
∴点P的坐标为(2,2)。
∵点P在反比例函数![]() 的图象上,∴
的图象上,∴![]() ,解得k=5。
,解得k=5。
(Ⅱ)∵在反比例函数![]() 图象的每一支上,y随x的增大而减小,
图象的每一支上,y随x的增大而减小,
∴k-1>0,解得k>1。
(Ⅲ)∵反比例函数![]() 图象的一支位于第二象限,
图象的一支位于第二象限,
∴在该函数图象的每一支上,y随x的增大而增大.
∵点A(x1,y1)与点B(x2,y2)在该函数的第二象限的图象上,且y1>y2,
∴x1>x2。
(1)设点P的坐标为(m,2),由点P在正比例函数y=x的图象上可求出m的值,从而得出P点坐标,再根据点P在反比例函数![]() 的图象上,所以
的图象上,所以![]() ,解得k=5。
,解得k=5。
(2)由于在反比例函数![]() 图象的每一支上,y随x的增大而减小,故k-1>0,求出k的取值范围即可。
图象的每一支上,y随x的增大而减小,故k-1>0,求出k的取值范围即可。
(3)反比例函数![]() 图象的一支位于第二象限,故在该函数图象的每一支上,y随x的增大而增大,所以A(x1,y1)与点B(x2,y2)在该函数的第二象限的图象上,且y1>y2,故可知x1>x2。
图象的一支位于第二象限,故在该函数图象的每一支上,y随x的增大而增大,所以A(x1,y1)与点B(x2,y2)在该函数的第二象限的图象上,且y1>y2,故可知x1>x2。

【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车去年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
【题目】某公司要把240吨白砂糖运往某市的A、B两地,用大小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种大小货车的载重分别是15吨/辆和10吨/辆,运往A地的运费为:大车630元/辆,小车420元/辆;运往B地的运费为:大车750元/辆,小车550元/辆.
(1)求大小两种货车各多少辆.
(2)如果安排10辆货车前往A地,其中调往A地的大货车有a辆,其余货车前往B地,填写下表:
前往A地 | 前往B地 | |
大货车/辆 | a | |
小货车/辆 |
(3)按照上表的分配方案,若设总费用为W,求W与a的关系式(用含a的代数式表示W)