题目内容
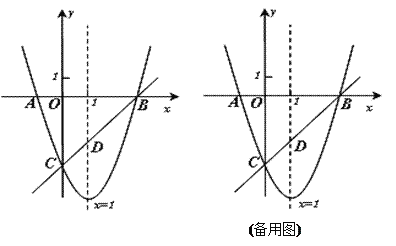
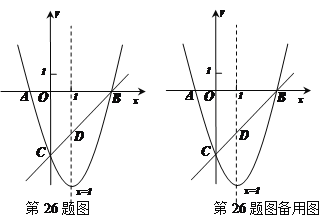
【题目】如图，已知抛物线y=x2＋bx＋c与x轴交于A、B两点（A点在B点左侧），与y轴交于点C（0，－3），对称轴是直线x=1，直线BC与抛物线的对称轴交于点D．
⑴求抛物线的函数表达式；
⑵求直线BC的函数表达式；
⑶点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P在第三象限．①当线段PQ=
AB时，求tan∠CED的值；②当以点C、D、E为顶点的三角形是直角三角形时，请直接写出点P的坐标．
【答案】(1)y=x2－2x－3 (2) y=x－3 (3) P（
，
）（1－
，－2），（1－
，
）
【解析】
已知了C点的坐标，即知道了OC的长，可在直角三角形BOC中根据∠BCO的正切值求出OB的长，即可得出B点的坐标．已知了△AOC和△BOC的面积比，由于两三角形的高相等，因此面积比就是AO与OB的比．由此可求出OA的长，也就求出了A点的坐标，然后根据A、B、C三点的坐标即可用待定系数法求出抛物线的解析式．
练习册系列答案
阅读快车系列答案
相关题目
