Question

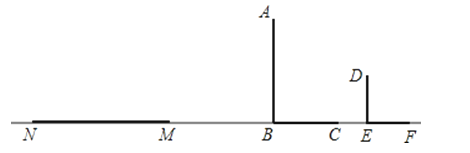
【题目】在数轴上，图中点A表示－36，点B表示44，动点P、Q分别从A、B两点同时出发，相向而行，动点P、Q的运动速度比之是3∶2（速度单位：1个单位长度/秒）．12秒后，动点P到达原点O，动点Q到达点C，设运动的时间为t（t＞0）秒．

（1）求OC的长；

（2）经过t秒钟，P、Q两点之间相距5个单位长度，求t的值；

（3）若动点P到达B点后，以原速度立即返回，当P点运动至原点时，动点Q是否到达A点，若到达，求提前到达了多少时间，若未能到达，说明理由．

Answer 1

【答案】（1）20；（2）t=15s或17s （3）s.

【解析】

（1）设P、Q速度分别为3m、2m，根据12秒后，动点P到达原点O列方程，求出P、Q的速度，由此即可得到结论．

（2）分两种情况讨论：①当A、B在相遇前且相距5个单位长度时；②当A、B在相遇后且相距5个单位长度时；列方程，求解即可．

（3）算出P运动到B再到原点时，所用的时间，再算出Q从B到A所需的时间，比较即可得出结论．

（1）设P、Q速度分别为3m、2m，根据题意得：12×3m=36，解得：m=1，∴P、Q速度分别为3、2，∴BC=12×2=24，∴OC=OB－BC=44－24=20．

（2）当A、B在相遇前且相距5个单位长度时：3t＋2t＋5=44＋36，5t=75，∴ t=15（s）；

当A、B在相遇后且相距5个单位长度时：3t＋2t－5=44＋36，5t=85，∴ t=17（s）．

综上所述：t=15s或17s．

（3）P运动到原点时，t==s，此时QB=2×=＞44+38=80，∴Q点已到达A点，∴Q点已到达A点的时间为：（s），故提前的时间为：－40=（s）．