Question

【题目】如图，⊙O为△ABC的内切圆，D、E、F分别为切点，已知∠C=90°，⊙O半径长为3cm，AC=10cm，则AD长度为cm．

Answer 1

【答案】7
【解析】解：连接OD、OE、OF，如图，设⊙O的半径为r，
∵⊙O为△ABC内切圆，与三边分别相切于D、E、F，
∴OD⊥AB，OE⊥BC，OF⊥AC，
∴四边形OECF为矩形
而OF=OE，
∴四边形OECF为正方形，
∴CE=OE=3，
∵AC=10，
∴AF=AC﹣CF=7，
∴AD=AF=7（cm）．
故答案为7．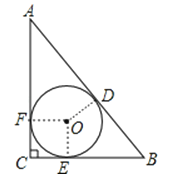

连接OD、OE、OF，如图，根据内切圆的定义和切线的性质得OD⊥AB，OE⊥BC，OF⊥AC，接着证明四边形OECF为正方形，则CE=OE=3，所以AF=AC﹣CF=7，然后根据切线长定理求AD．