题目内容
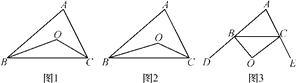
【题目】如图,点D是△ABC内部的一点,BD=CD,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,且BE=CF.求证:AB=AC.

【答案】证明见解析.
【解析】
欲证明AB=AC,只要证明∠ABC=∠ACB即可,根据“HL”证明Rt△BDE≌Rt△CDF,由全等三角形的性质可证∠EBD=∠FCD,再由等腰三角形的性质∠DBC=∠DCB,从而可证∠ABC=∠ACB.
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
在Rt△BDE和Rt△CDF中,
![]()
∴Rt△BDE≌Rt△CDF(HL),
∴∠EBD=∠FCD,
∵BD=CD,
∴∠DBC=∠DCB,
∴∠DBC+∠EBD=∠DCB+∠FCD,
即∠ABC=∠ACB,
∴AB=AC.

 名校课堂系列答案
名校课堂系列答案【题目】为了解学生对安全知识的掌握情况,学校随机抽取了20名学生进行安全知识测试,测试成绩(百分制)如下:
78、86、93、81、97、88、79、93、87、90、93、98、88、81、94、95、81、98、99、94
(1)根据上述数据,将下列表格补充完整(每组含最小值):
成绩/分 | 70~80 | 80~90 | 90~100 |
人数 | 7 |
(2)若用(1)中数据制作扇形统计图,求出表示“70~80”扇形的圆心角度数;
(3)已知该校共有2000名学生,若规定成绩90分及以上为优秀,估计该校学生对安全知识掌握情况为优秀的有多少人?
【题目】“十九大”报告提出了我国将加大治理环境污染的力度,还我青山绿水,其中雾霾天气让环保和健康问题成为焦点,为了调查学生对雾霾天气知识的了解程度,某校在全校学生中抽取400名同学做了一次调查,根据调查统计结果,绘制了不完整的一种统计图表.
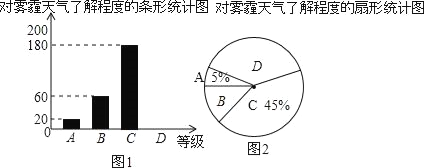
对雾霾了解程度的统计表
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题:
(1)统计表中:m= ,n= ;
(2)请在图1中补全条形统计图;
(3)请问在图2所示的扇形统计图中,D部分扇形所对应的圆心角是多少度?