题目内容
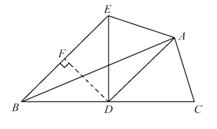
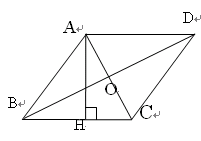
如图,已知AD是△ABC的中线,∠ADC=45°,把△ABC沿AD对折,点C落在点E的位置,连接BE,若BC=6cm。
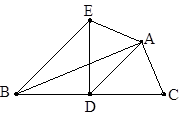
(1)求BE的长;
(2)当AD=4cm时,求四边形BDAE的面积。
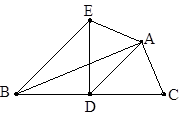
(1)求BE的长;
(2)当AD=4cm时,求四边形BDAE的面积。
解:(1)由题意,有ED=DC,∠ADE=∠ADC=45°,∴∠EDC=90°. ……1分
又AD为△ABC的中线,∴CD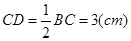 ,ED=DC=BD=3(cm).
,ED=DC=BD=3(cm).
在Rt△BDE中,由勾股定理,有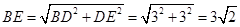 (cm). ……2分
(cm). ……2分
(2)在Rt△BDE中,∵BD=DE,∴∠EBD=45°.∴∠EBD=∠ADC=45°.
∴BE∥AD.∴BDAE是梯形. ……2分
过D作DF⊥BE于点F.
在Rt△BDE中,有
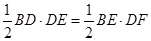
∴DF=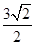 (cm). ……1分
(cm). ……1分
∴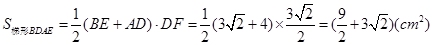 ……2分
……2分
又AD为△ABC的中线,∴CD
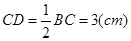 ,ED=DC=BD=3(cm).
,ED=DC=BD=3(cm).在Rt△BDE中,由勾股定理,有
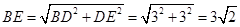 (cm). ……2分
(cm). ……2分(2)在Rt△BDE中,∵BD=DE,∴∠EBD=45°.∴∠EBD=∠ADC=45°.
∴BE∥AD.∴BDAE是梯形. ……2分
过D作DF⊥BE于点F.

在Rt△BDE中,有
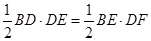
∴DF=
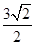 (cm). ……1分
(cm). ……1分∴
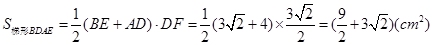 ……2分
……2分(1)由折叠可知:△ADC≌△ADE,∠EDC=2∠ADC=90°,ED=DC,又BD=DC,△BDE是等腰直角三角形,可求BE长;
(2)由(1)知,∠BED=45°,∠EDA=45°,∴四边形BDAE是梯形,已知上底AD=4,下底BE="3" 2,为求梯形高,过D作DF⊥BE于点F,DF实际上就是等腰直角三角形BDE斜边上的高,可求长度.
(2)由(1)知,∠BED=45°,∠EDA=45°,∴四边形BDAE是梯形,已知上底AD=4,下底BE="3" 2,为求梯形高,过D作DF⊥BE于点F,DF实际上就是等腰直角三角形BDE斜边上的高,可求长度.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
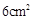 ,长为
,长为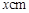 ,则这个矩形的宽
,则这个矩形的宽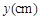 与长
与长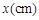 的函数关系为 。
的函数关系为 。