题目内容
【题目】在ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC= ![]() ,则ABCD的面积是 .
,则ABCD的面积是 . 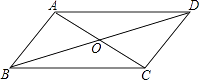
【答案】24
【解析】解:作OE⊥CD于E,如图所示: ∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD= ![]() BD=5,CD=AB=4,
BD=5,CD=AB=4,
∵sin∠BDC= ![]() =
= ![]() ,
,
∴OE=3,
∴DE= ![]() =4,
=4,
∵CD=4,
∴点E与点C重合,
∴AC⊥CD,OC=3,
∴AC=2OC=6,
∴ABCD的面积=CDAC=4×6=24;
所以答案是:24.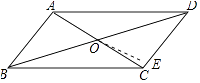
【考点精析】关于本题考查的平行四边形的性质和解直角三角形,需要了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目