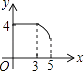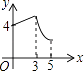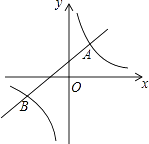��Ŀ����
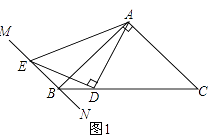
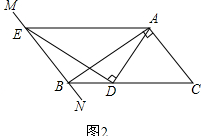
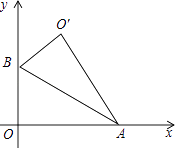
����Ŀ������45��ǵ����ǰ��ֱ�Ƕ���R����ֱ��l�ϣ��ֱ������ǵĶ���M��N��l�Ĵ��ߣ�����ֱ�ΪP��Q��
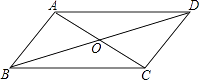
��1����ͼ1���۲�ͼ1��֪����NQ��ȵ��߶��� �� ���NPQ��ȵĽ��� �� 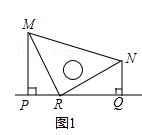
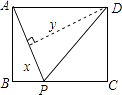
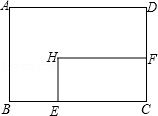
��2��ֱ�ǡ�ABC�У���B=90�㣬��AB������ȡһ��D������CD���ֱ���AC��DCΪ����������ACEF��������CDGH����ͼ2����E��H�ֱ���BC����ֱ�ߵĴ��ߣ�����ֱ�ΪK��L����̽��EK��HL֮���������ϵ����֤����Ľ��ۣ�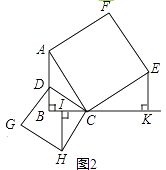
��3��ֱ�ǡ�ABC�У���B=90�㣬��AB������ȡһ��D������CD���ֱ���AC��DCΪ��������ACEF�;���CDGH������EH��BC���ڵ�ֱ���ڵ�T����ͼ3�����AC=kCE��CD=kCH����̽��TE��TH֮���������ϵ����֤����Ľ��ۣ�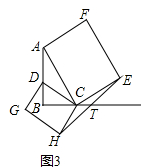
���𰸡�
��1��PR����PMR
��2��
�⣺���ı���ACEF�������Σ�
��AC=CE����ACE=90�㣬
��EK��BK��
���B=��EKC=90�㣬
���BAC+��ACB=��ACB+��ECK=90�㣬
���BAC=��ECK��
�ڡ�ABC���CEK�У�  ��
��
���ABC�ա�CEK��
��EK=BC��
���ı���CDGH�������Σ���CD=CH����DCH=90�㣬
��HI��BC��
���B=��CIH=90�㣬
���DCB+��ICK=��ICK+��CHI=90�㣬���DCB=��CHI��
�ڡ�DCB���CHI�У� 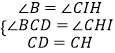 �����DCB�ա�CHI��
�����DCB�ա�CHI��
��BC=HI��
��EK=IH
��3��
�⣺��ͼ3����E��EM��BC��M����H��HN��BC��N��
���ı���ACEF�Ǿ��Σ�
���ACE=90�㣬
���BAC+��ACB=��ACB+��ECM=90�㣬
���BAC=��ECM�����ACB�ס�ECM��
�� ![]() =k��
=k��
��BC=kEM��
ͬ����BCD�ס�NHC��
�� ![]() =K��
=K��
��BC=kHN��
��EM=HN��
�ڡ�NHT���EMT�У� 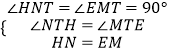 ��
��
���NHT�ա�EMT��
��ET=HT��
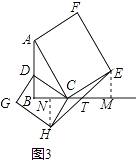
���������⣺��1���ߡ�MRN�ǵ���ֱ�������Σ�
��MR=RN����MRN=90�㣬
��MP��PQ��NQ��PQ��
���MPR=��NQ=90�㣬
���PMR+��MRP=��MRP+��NRQ=90�㣬
���PMR=��NRQ��
�ڡ�MPR���NRQ�У� 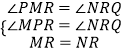 ��
��
���MPR�ա�NRQ��
��QN=PR����NRQ=��PMR��
���Դ��ǣ�PR����PMR��
�����㾫�������յ���ֱ�������κ�ȫ�������ε������ǽ����ĸ�������Ҫ֪������ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ�

 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д� �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�