题目内容
【题目】完成下列各题:
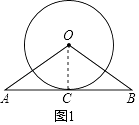
(1)如图,已知直线AB与⊙O相切于点C,且AC=BC,求证:OA=OB. 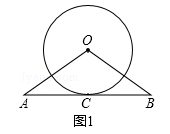
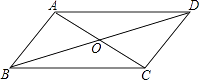
(2)如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=3,求AC的长. 
【答案】
(1)证明:连接OC,
∵直线AB与⊙O相切于点C,
∴OC⊥AB,
又∵AC=BC,
∴OC垂直平分AB,
∴OA=OB
(2)证明:∵四边形ABCD是矩形,
∴AC=BD,OA=OC= ![]() AC,BO=DO=
AC,BO=DO= ![]() BD,∠BAD=90°,
BD,∠BAD=90°,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,∠ADB=30°,
∴AC=BD=2AB=6cm
【解析】(1)根据线段垂直平分线的性质:线段垂直平分线上的点到两端点的距离相等来证明;(2)根据矩形性质得出AC=BD,OA=OB,求出∠AOB=60°,得出△AOB是等边三角形,求出∠ADB=30°,得出AC=BD=2AB=6cm即可.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目