��Ŀ����
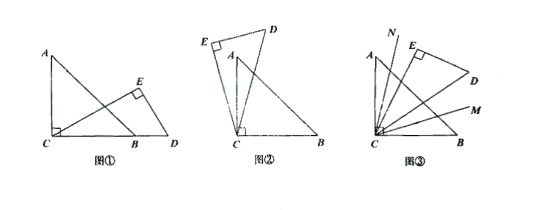
����Ŀ����ͼ����һ��ֱ�����ǰ���30������Ƕ�������һ��ֱ�����ǰ��ֱ�Ƕ������һ��.��ע����ACB����DEC��ֱ�ǣ���A=45�㣬��DEC=30�㣩.
��1����ͼ�٣�����C��B��D��һ��ֱ���ϣ�����ACE�Ķ�����
��2����ͼ�ڣ���ֱ�����ǰ�CDE�Ƶ�c��ʱ�뷽��ת����ij��λ�ã���ǡ��ƽ����DCE������BCD�Ķ�����
��3����ͼ������DECʼ������ACB���ڲ����ֱ�������CMƽ����BCD,����CNƽ����ACE.������ǰ�DCE����ACB���Ƶ�C����ת������MCN�Ķ����Ƿ����仯��������䣬������Ķ���������仯��˵��������
���𰸡���1��60������2��75������3�����䣬60��
��������
��1�����á�ACE=��BCA-��DCE���м��㣻
��2������CAǡ��ƽ�֡�DCE�õ���DCA=![]() ��DCE=15����Ȼ����ݡ�BCD=��BCA-��DCA���м��㣻
��DCE=15����Ȼ����ݡ�BCD=��BCA-��DCA���м��㣻
��3���ȸ���CMƽ�֡�BCD��CNƽ�֡�ACE�õ���ECN=![]() ��ACE����DCM=
��ACE����DCM=![]() ��BCD�����ECN+��DCM=
��BCD�����ECN+��DCM=![]() ����BCA-��DCE�������ԡ�MCN=��ECN+��DCM+��DCE=
����BCA-��DCE�������ԡ�MCN=��ECN+��DCM+��DCE=![]() ����BCA+��DCE����Ȼ��ѡ�BCA=90�㣬��DCE=30��������㼴�ɣ�
����BCA+��DCE����Ȼ��ѡ�BCA=90�㣬��DCE=30��������㼴�ɣ�
�⣺��1���ߡ�BCA=90�㣬��DCE=30�㣬
���ACE=��BCA-��DCE=60�㣻
��2����CAǡ��ƽ�֡�DCE��
���DCA=![]() ��DCE=
��DCE=![]() ��30��=15�㣬
��30��=15�㣬
���BCD=��BCA-��DCA=90��-15��=75�㣻
��3����MCN�Ķ����������仯����MCN=60�����������£�
��CMƽ�֡�BCD��CNƽ�֡�ACE��
���ECN=![]() ��ACE����DCM=
��ACE����DCM=![]() ��BCD��
��BCD��
���ECN+��DCM=![]() ����ACE+��BCD��=
����ACE+��BCD��=![]() ����BCA-��DCE����
����BCA-��DCE����
���MCN=��ECN+��DCM+��DCE
=![]() ����BCA+��DCE��=
����BCA+��DCE��=![]() ����90��+30�㣩=60�㣮
����90��+30�㣩=60�㣮