题目内容
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() 与
与![]() 交于点
交于点 ![]() ,
,![]() 为
为![]() 延长线上的一点,且
延长线上的一点,且![]() ,连接
,连接![]() 分别交
分别交![]() ,
,![]() 于点
于点 ![]() ,
,![]() ,连接
,连接![]() ,则下列结论中一定成立的是__________.
,则下列结论中一定成立的是__________.
①![]() ;②与
;②与![]() 全等的三角形共有5个;③
全等的三角形共有5个;③![]() ;④由点
;④由点![]() 、
、![]() 、
、![]() 、
、![]() 构成的四边形是菱形
构成的四边形是菱形
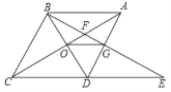
【答案】①④
【解析】
由AAS证明△ABG≌△DEG,得出AG=DG,证出OG是△ACD的中位线,得出OG=![]() CD=
CD=![]() AB,①正确;
AB,①正确;
先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,④正确;
由菱形的性质得得出△ABG≌△BDG≌△DEG,由SAS证明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正确;
证出OG是△ABD的中位线,得出OG∥AB,OG=![]() AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;③不正确;即可得出结果.
AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;③不正确;即可得出结果.
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
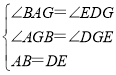 ,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ACD的中位线,
∴OG=![]() CD=
CD=![]() AB,①正确;
AB,①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,④正确;
∴AD⊥BE,
由菱形的性质得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中,
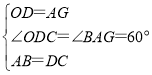 ,
,
∴△ABG≌△DCO(SAS),
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,②不正确;
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG∥AB,OG=![]() AB,
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∴△GOD的面积=![]() △ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△AOG的面积=△BOG的面积,
∴S四边形ODGF=S△ABF;③不正确;
正确的是①④.
故答案为:①④.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案