题目内容
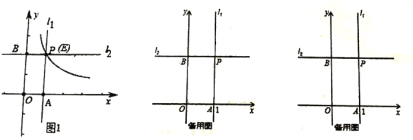
【题目】定义:在平面直角坐标系中,O为坐标原点,设点P的坐标为(x,y),当x<0时,点P的变换点P′的坐标为(﹣x,y);当x≥0时,点P的变换点P′的坐标为(﹣y,x).
(1)若点A(2,1)的变换点A′在反比例函数y=![]() 的图象上,则k= ;
的图象上,则k= ;
(2)若点B(2,4)和它的变换点B'在直线y=ax+b上,则这条直线对应的函数关系式为 ,∠BOB′的大小是 度.
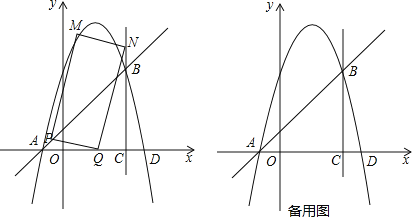
(3)点P在抛物线y=x2﹣2x﹣3的图象上,以线段PP′为对角线作正方形PMP'N,设点P的横坐标为m,当正方形PMP′N的对角线垂直于x轴时,求m的取值范围.
(4)抛物线y=(x﹣2)2+n与x轴交于点C,D(点C在点D的左侧),顶点为E,点P在该抛物线上.若点P的变换点P′在抛物线的对称轴上,且四边形ECP′D是菱形,求n的值.
【答案】(1) -2;(2) y=![]() x+
x+![]() ,90;(3) m<0,m=
,90;(3) m<0,m=![]() 或m=
或m=![]() ;(4) n=﹣8,n=﹣2,n=﹣3.
;(4) n=﹣8,n=﹣2,n=﹣3.
【解析】
(1)先求出A的变换点A′,然后把A′代入反比例函数即可得到结论;
(2)确定点B′的坐标,把问题转化为方程组解决;
(3)分三种情形讨论:①当m<0时;②当m≥0,PP'⊥x轴时;③当m≥0,MN⊥x轴时.
(4)利用菱形的性质,得到点E与点P'关于x轴对称,从而得到点P'的坐标为(2,﹣n).分两种情况讨论:①当点P在y轴左侧时,点P的坐标为(﹣2,﹣n),代入抛物线解析式,求解即可;②当点P在y轴右侧时,点P的坐标为(﹣n,﹣2).代入抛物线解析式,求解即可.
(1)∵A(2,1)的变换点为A′(-1,2),把A′(-1,2)代入y=![]() 中,得到k=-2.
中,得到k=-2.
故答案为:-2.
(2)点B(2,4)的变换点B′(﹣4,2),把(2,4),(﹣4,2)代入y=ax+b中.
得到:![]() ,解得:
,解得: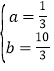 ,∴
,∴![]() .
.
∵OB2=![]() =20,OB′2=
=20,OB′2=![]() =20,BB′2=
=20,BB′2=![]() =40,∴OB2+OB′2=BB′2,∴∠BOB′=90°.
=40,∴OB2+OB′2=BB′2,∴∠BOB′=90°.
故答案为:y=![]() x+
x+![]() ,90.
,90.
(3)①当m<0时,点P与点P'关于y轴对称,此时MN垂直于x 轴,所以m<0.
②当m≥0,PP'⊥x轴时,则点P'的坐标为(m,m),点P的坐标为(m,﹣m).
将点P(m,﹣m)代入y=x2﹣2x﹣3,得:﹣m=m2﹣2m﹣3.
解得:![]() (不合题意,舍去).
(不合题意,舍去).
所以![]() .
.
③当m≥0,MN⊥x轴时,则PP'∥x轴,点P的坐标为(m,m).
将点P(m,m)代入y=x2﹣2x﹣3,得:m=m2﹣2m﹣3.
解得:![]() (不合题意,舍去).
(不合题意,舍去).
所以![]() .
.
综上所述:m的取值范围是m<0,m=![]() 或m=
或m=![]() .
.
(4)∵四边形ECP'D是菱形,∴点E与点P'关于x轴对称.
∵点E的坐标为(2,n),∴点P'的坐标为(2,﹣n).
①当点P在y轴左侧时,点P的坐标为(﹣2,﹣n).
代入y=(x﹣2)2+n,得:﹣n=(﹣2﹣2)2+n,解得:n=﹣8.
②当点P在y轴右侧时,点P的坐标为(﹣n,﹣2).
代入y=(x﹣2)2+n,得:﹣2=(﹣n﹣2)2+n.解得:n1=﹣2,n2=﹣3.
综上所述:n的值是n=﹣8,n=﹣2,n=﹣3.

【题目】某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛,特为甲、乙两名队员举行了一次选拔赛,要求这两名队员各射击10次.比赛结束后,根据比赛成绩情况,将甲、乙两名队员的比赛成绩制成了如下的统计表:
甲队员成绩统计表
成绩(环) | 7 | 8 | 9 | 10 |
次数(次) | 5 | 1 | 2 | 2 |
乙队员成绩统计表
成绩(环) | 7 | 8 | 9 | 10 |
次数(次) | 4 | 3 | 2 | 1 |
(1)经过整理,得到的分析数据如表,求表中的![]() ,
,![]() ,
,![]() 的值.
的值.
队员 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 8 | 7.5 | 7 |
|
乙 |
|
| 7 | 1 |
(2)根据甲、乙两名队员的成绩情况,该射击队准备选派乙参加比赛,请你写出一条射击队选派乙的理由.