题目内容
【题目】某校七、八年级各有300名学生,近期对他们“2020年新型冠状病毒”防治知识进行了线上测试,为了了解他们的掌握情况,从七、八年级各随机抽取了50名学生的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息:
a.七年级的频数分布直方图如下(数据分为5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):

b.七年级学生成绩在80≤x<90的这一组是:
80 80.5 81 82 82 83 83.5 84
84 85 86 86.5 87 88 89 89
c.七、八年级学生成绩的平均数、中位数、众数如下:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 85.3 | m | 90 |
八年级 | 87.2 | 85 | 91 |
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)在随机抽样的学生中,防治知识成绩为84分的学生,在 年级排名更靠前,理由是 ;
(3)若各年级防治知识的前90名将参加线上防治知识竞赛,预估七年级分数至少达到 分的学生才能入选;
(4)若85分及以上为“优秀”,请估计七年级达到“优秀”的人数.
【答案】(1)82;(2)七,理由见解析;(3)至少达到89分才能入选;(4)120人
【解析】
(1)根据七年级的频数分布直方图以及七年级学生成绩在80≤x<90的这一组的数据可知第25,26名学生的成绩为82,82,所以![]() ;
;
(2)根据84分与七、八年级的中位数对比即可得出答案;
(3)先计算90名学生占七年级总人数的比例,再乘以参与抽查的人数50人,即可得出50名参与抽查学生中前15名可入选,再根据七年级的频数分布直方图可知90≤x≤100有13名,则在 80≤x<90这一组的数据中选取成绩最好的两名即可,从而得出结论;
(4)七年级总人数乘以85分以上人数占参与抽查的总人数即可.
解:(1)由题意可得:
第25,26名学生的成绩为82,82,所以![]()
故答案为:82;
(2)因为该学生的成绩大于七年级成绩的中位数,而小于八年级成绩的中位数,因此,防治知识成绩为84分的学生,在七年级排名更靠前;
故答案为:七,该学生的成绩大于七年级成绩的中位数,而小于八年级成绩的中位数;
(3)![]() (人)
(人)
∵成绩在90≤x≤100段学生有13名,则在 80≤x<90段选取成绩最好的两名
∴故至少达到89分才能入选.;
故答案为:89;
(4) ![]() (人)
(人)
∴七年级达到优秀的人数约为120人.

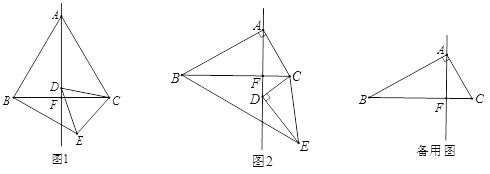
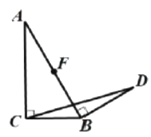
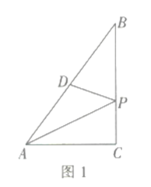
【题目】如图1,在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() .若
.若![]() 设
设 ![]() (当点
(当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为
的值为![]() ),
),![]() .
.
小明根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.
![]() 通过取点、画图、计算,得到了
通过取点、画图、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
说明:补全表格时,相关数值保留一位小数.
(参考数据:![]() ) .
) .
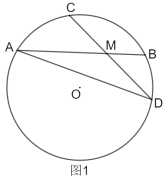
![]() 如图2,描出剩余的点,并用光滑的曲线画出该函数的图象.
如图2,描出剩余的点,并用光滑的曲线画出该函数的图象.
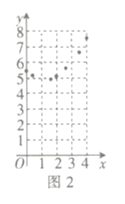
![]() 观察图象,下列结论正确的有 _ .
观察图象,下列结论正确的有 _ .
①函数有最小值,没有最大值
②函数有最小值,也有最大值
③当![]() 时,
时,![]() 随着
随着![]() 的增大而增大
的增大而增大
④当![]() 时,
时,![]() 随着
随着![]() 的增大而减小
的增大而减小