题目内容
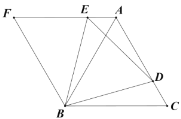
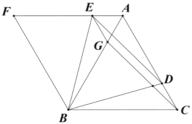
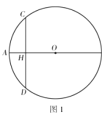
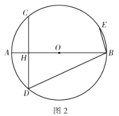
【题目】在直角坐标系中,已知抛物线![]() (a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知
(a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知![]() :S四边形ACBD=1:4.
:S四边形ACBD=1:4.
(1)求点D的坐标(用仅含c的代数式表示);
(2)若tan∠ACB=![]() ,求抛物线的解析式.
,求抛物线的解析式.
【答案】(1)D(2,![]() );(2)抛物线的解析式为:
);(2)抛物线的解析式为:![]() ,或
,或![]() ,或
,或![]() .
.
【解析】
(1)直接代入顶点坐标公式化简即可;
(2)先由![]() :S四边形ACBD=1:4,得到等底三角形的面积之比
:S四边形ACBD=1:4,得到等底三角形的面积之比![]() :
:![]() =1:3,而求出
=1:3,而求出![]() ,解析式化为
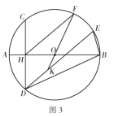
,解析式化为![]() ,求得A(1,0),B(3,0),过点B作
,求得A(1,0),B(3,0),过点B作![]() 的延长线于点H,得到
的延长线于点H,得到![]() ∽
∽![]() ,依据相似的性质、锐角三角函数,用c表示AH、BH,最后在三角形ABH中依据勾股定理求出c,即可得到解析式.
,依据相似的性质、锐角三角函数,用c表示AH、BH,最后在三角形ABH中依据勾股定理求出c,即可得到解析式.
解:(1)抛物线![]() 的顶点D的坐标为
的顶点D的坐标为![]()
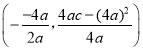 ,
,
∴顶点D的坐标为(2,![]() );
);
(2)∵![]() 与y轴负半轴交于点C,
与y轴负半轴交于点C,
∴C(0,c),![]() ,
,
过点D作![]() 轴于点G,则
轴于点G,则![]()
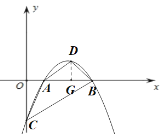
∵![]() :S四边形ACBD=1:4,
:S四边形ACBD=1:4,
∴![]() :
:![]() =1:3,
=1:3,
则![]() ,即
,即![]() ,
,
∴![]() ,
,
∴抛物线的解析式为:![]() 或
或![]() ,
,![]() =
=![]() ,
,![]() ,
,
∴令![]() =0,解得
=0,解得![]()
∴A(1,0),B(3,0),![]() ,
,
过点B作![]() 的延长线于点H,
的延长线于点H,
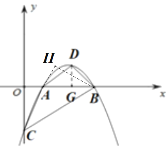
∴![]() (对顶角相等),
(对顶角相等),
∴![]() ∽
∽![]() ,tan∠ACB=
,tan∠ACB=![]() =
=![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴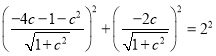 ,
,
∴![]() =0,(
=0,(![]() )
)
∴![]() -1或-3或-2+
-1或-3或-2+![]() (舍)或-2-
(舍)或-2-![]() ,
,
∴抛物线的解析式为:![]() ,或
,或![]() ,或
,或![]() .
.

 53随堂测系列答案
53随堂测系列答案【题目】某校七、八年级各有300名学生,近期对他们“2020年新型冠状病毒”防治知识进行了线上测试,为了了解他们的掌握情况,从七、八年级各随机抽取了50名学生的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息:
a.七年级的频数分布直方图如下(数据分为5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):

b.七年级学生成绩在80≤x<90的这一组是:
80 80.5 81 82 82 83 83.5 84
84 85 86 86.5 87 88 89 89
c.七、八年级学生成绩的平均数、中位数、众数如下:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 85.3 | m | 90 |
八年级 | 87.2 | 85 | 91 |
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)在随机抽样的学生中,防治知识成绩为84分的学生,在 年级排名更靠前,理由是 ;
(3)若各年级防治知识的前90名将参加线上防治知识竞赛,预估七年级分数至少达到 分的学生才能入选;
(4)若85分及以上为“优秀”,请估计七年级达到“优秀”的人数.