题目内容
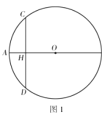
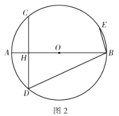
【题目】已知：⊙O的两条弦
，
相交于点
，且
．
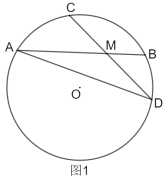
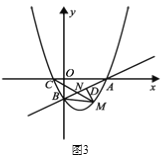
（1）如图1，连接
，求证：
．
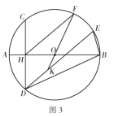
（2）如图2，在
，在
上取一点
，使得
，
交于点
，连接
．
①判断
与
是否相等，并说明理由．
②若
，
，求
的面积．
【答案】（1）见解析；（2）①相等，理由见解析；②
．
【解析】
（1）根据弦，弧之间的关系得出
，进而有
，然后根据圆周角定理的推论即可得出
，则结论可证；
（2）①连接AC，首先证明
≌
，则有
，然后根据
，
和等量代换即可得出结论；
（3）设
，则
，然后利用DM=x+7和AM=DM建立一个关于x的方程，解方程即可求出x的值，从而AM可求，最后利用
即可求解．
（1）∵
，
，
，
∴，
∴
；
（2）①相等，理由如下：
如图：连接AC，
∴
，
又∵
，
∴
，
又∵AM=AM，
∴≌（ASA）
∴，
又∵，
∴
；
②由（1）知AM=DM，
设，
，
，
由①知：，
∴
，
∵DE=7，
∴DF=7，
则：DM=x+7，
由AM=DM，得：17－x=x+7，解得：x=5,
∴AM=17－5=12，
∴
．
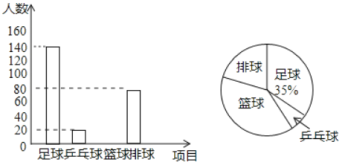
【题目】某校七、八年级各有300名学生，近期对他们“2020年新型冠状病毒”防治知识进行了线上测试，为了了解他们的掌握情况，从七、八年级各随机抽取了50名学生的成绩（百分制），并对数据（成绩）进行整理、描述和分析．下面给出了部分信息：
a．七年级的频数分布直方图如下（数据分为5组：50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）：
b．七年级学生成绩在80≤x＜90的这一组是：
80 80.5 81 82 82 83 83.5 84
84 85 86 86.5 87 88 89 89
c．七、八年级学生成绩的平均数、中位数、众数如下：
年级 | 平均数 | 中位数 | 众数 |
七年级 | 85.3 | m | 90 |
八年级 | 87.2 | 85 | 91 |
根据以上信息，回答下列问题：
（1）表中m的值为 ；
（2）在随机抽样的学生中，防治知识成绩为84分的学生，在 年级排名更靠前，理由是 ；
（3）若各年级防治知识的前90名将参加线上防治知识竞赛，预估七年级分数至少达到 分的学生才能入选；
（4）若85分及以上为“优秀”，请估计七年级达到“优秀”的人数．
