题目内容
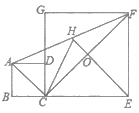
【题目】已知四边形![]() 和四边形
和四边形![]() 都是正方形,且
都是正方形,且![]() .
.
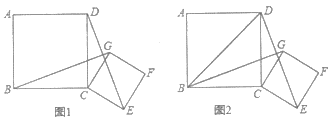
(1)如图1,连接![]() 、
、![]() .求证:
.求证:![]() ;
;
(2)如图2,将正方形![]() 绕着点
绕着点![]() 旋转到某一位置时恰好使得
旋转到某一位置时恰好使得![]() ,
,![]() .求
.求![]() 的度数;
的度数;
(3)在(2)的条件下,当正方形![]() 的边长为
的边长为![]() 时,请直接写出正方形
时,请直接写出正方形![]() 的边长.
的边长.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据正方形的性质可得![]() ,CG=CE,∠BCD=∠GCE=90°,然后利用SAS即可证出
,CG=CE,∠BCD=∠GCE=90°,然后利用SAS即可证出![]() ≌
≌![]() ,从而得出结论;
,从而得出结论;
(2)连接![]() ,由
,由![]() ,
,![]() ,得:
,得:![]() ,利用SAS证出
,利用SAS证出 ![]() ,从而证出
,从而证出![]() 是等边三角形,得出
是等边三角形,得出![]() ,即可求出结论;
,即可求出结论;
(3)过点G作GM⊥BC,交BC的延长线于点M,设CM=x,则GM=x,CG=![]() x,在Rt△BGM中,根据勾股定理,列出方程,即可求解.
x,在Rt△BGM中,根据勾股定理,列出方程,即可求解.
证明:(1)∵四边形![]() 和
和![]() 是正方形
是正方形
∴![]() ,CG=CE,∠BCD=∠GCE=90°
,CG=CE,∠BCD=∠GCE=90°
∴∠BCD+DCG=∠GCE+DCG
∴![]()
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ≌
≌![]() .
.
∴![]() ;
;
(2)解:如图连接![]() ,
,

![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
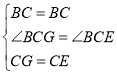 ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形.
是等边三角形.
∴![]() ;
;
∵![]()
∴![]() .
.
(3)解:过点G作GM⊥BC,交BC的延长线于点M,如图2,
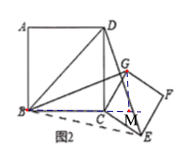
∵![]() ,
,
∴∠GCM=45°,
设CM=x,则GM=x,CG=![]() x,
x,
∵正方形![]() 的边长为
的边长为![]() ,
,
∴BC=![]() ,BG=BD=4,
,BG=BD=4,
∵在Rt△BGM中,BM2+GM2=BG2,
∴![]() ,
,
解得:![]() ,
,![]() (舍)
(舍)
∴![]() ,
,
即:正方形![]() 的边长是:
的边长是:![]() .
.

 阅读快车系列答案
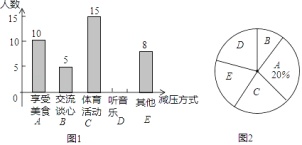
阅读快车系列答案【题目】某校七、八年级各有300名学生,近期对他们“2020年新型冠状病毒”防治知识进行了线上测试,为了了解他们的掌握情况,从七、八年级各随机抽取了50名学生的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息:
a.七年级的频数分布直方图如下(数据分为5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):

b.七年级学生成绩在80≤x<90的这一组是:
80 80.5 81 82 82 83 83.5 84
84 85 86 86.5 87 88 89 89
c.七、八年级学生成绩的平均数、中位数、众数如下:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 85.3 | m | 90 |
八年级 | 87.2 | 85 | 91 |
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)在随机抽样的学生中,防治知识成绩为84分的学生,在 年级排名更靠前,理由是 ;
(3)若各年级防治知识的前90名将参加线上防治知识竞赛,预估七年级分数至少达到 分的学生才能入选;
(4)若85分及以上为“优秀”,请估计七年级达到“优秀”的人数.