МвДїДЪИЭ
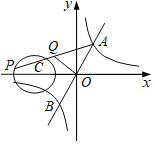
ЎѕМвДїЎїИзНј1Ј¬ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() ОЄ
ОЄ![]() µДЦРµгЈ¬
µДЦРµгЈ¬![]() КЗ
КЗ![]() ±ЯЙПТ»¶ЇµгЈ¬Б¬ЅУ
±ЯЙПТ»¶ЇµгЈ¬Б¬ЅУ![]() Ј®Иф
Ј®Иф![]() Йи
Йи ![]() (µ±µг
(µ±µг![]() Улµг
Улµг![]() ЦШєПК±Ј¬
ЦШєПК±Ј¬![]() µДЦµОЄ
µДЦµОЄ![]() )Ј¬
)Ј¬![]() Ј®
Ј®
РЎГчёщѕЭС§П°єЇКэµДѕСйЈ¬¶ФєЇКэ![]() ЛжЧФ±дБї
ЛжЧФ±дБї![]() µД±д»Ї¶ш±д»ЇµД№жВЙЅшРРБЛМЅѕїЈ®
µД±д»Ї¶ш±д»ЇµД№жВЙЅшРРБЛМЅѕїЈ®
ПВГжКЗРЎГчµДМЅѕї№эіМЈ¬ЗлІ№ідНкХыЈ®
![]() НЁ№эИЎµгЎў»НјЎўјЖЛгЈ¬µГµЅБЛ
НЁ№эИЎµгЎў»НјЎўјЖЛгЈ¬µГµЅБЛ![]() Ул
Ул![]() µДјёЧйЦµЈ¬ИзПВ±нЈє
µДјёЧйЦµЈ¬ИзПВ±нЈє
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЛµГчЈєІ№И«±нёсК±Ј¬Па№ШКэЦµ±ЈБфТ»О»РЎКэЈ®
(ІОїјКэѕЭЈє![]() ) Ј®
) Ј®
![]() ИзНј2Ј¬ГиіцКЈУаµДµгЈ¬ІўУù⻬µДЗъПЯ»іцёГєЇКэµДНјПуЈ®
ИзНј2Ј¬ГиіцКЈУаµДµгЈ¬ІўУù⻬µДЗъПЯ»іцёГєЇКэµДНјПуЈ®
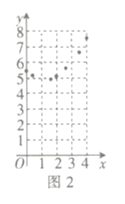
![]() №ЫІмНјПуЈ¬ПВБРЅбВЫХэИ·µДУР _ Ј®
№ЫІмНјПуЈ¬ПВБРЅбВЫХэИ·µДУР _ Ј®
ўЩєЇКэУРЧоРЎЦµЈ¬Г»УРЧоґуЦµ
ўЪєЇКэУРЧоРЎЦµЈ¬ТІУРЧоґуЦµ
ўЫµ±![]() К±Ј¬
К±Ј¬![]() ЛжЧЕ
ЛжЧЕ![]() µДФцґу¶шФцґу
µДФцґу¶шФцґу
ўЬµ±![]() К±Ј¬
К±Ј¬![]() ЛжЧЕ
ЛжЧЕ![]() µДФцґу¶шјхРЎ
µДФцґу¶шјхРЎ
Ўѕґр°ёЎїЈЁ1Ј©5.0Ј»6.0Ј»ЈЁ2Ј©јыЅвОцЈ»ЈЁ3Ј©ўЪўЫЈ®
ЎѕЅвОцЎї
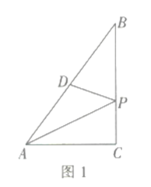
ЈЁ1Ј©№эµгDЧчDEЎНBCЈ¬ФтDE=![]() Ј¬УЙ№ґ№Й¶ЁАнЗуіцPAєНPDµДі¤¶ИЈ¬јґїЙµГµЅґр°ёЈ»
Ј¬УЙ№ґ№Й¶ЁАнЗуіцPAєНPDµДі¤¶ИЈ¬јґїЙµГµЅґр°ёЈ»
ЈЁ2Ј©ёщѕЭМвТвЈ¬НЁ№эГиµгЎўБ¬ПЯЈ¬І№И«єЇКэНјПсјґїЙЈ»
ЈЁ3Ј©ЅбєПєЇКэНјПсЈ¬·Ц±р¶ФЛДёцСЎПоЅшРРЕР¶ПЈ¬јґїЙµГµЅґр°ёЈ®
ЅвЈєЈЁ1Ј©µ±![]() К±Ј¬ИзНјЈє
К±Ј¬ИзНјЈє
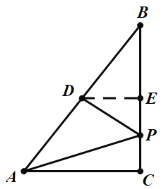
ЎЯAC=3Ј¬PC=1Ј¬УЙ№ґ№Й¶ЁАнЈ¬µГ
![]() Ј¬
Ј¬
ЎЯµгDКЗABЦРµгЈ¬DEЎНBCЈ¬ЎПACB=90ЎгЈ¬
ЎаDEКЗЦРО»ПЯЈ¬
ЎаDE=![]() Ј¬CE=2Ј¬
Ј¬CE=2Ј¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј»
Ј»
µ±PC=3К±Ј¬ґЛК±PE=1Ј¬ИзНјЈє
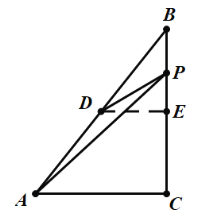
Ўа![]() Ј¬
Ј¬![]() Ј¬
Ј¬
Ўа![]() Ј»
Ј»
№Кґр°ёОЄЈє![]() Ј»
Ј»![]() Ј®
Ј®
![]() ГиµгЎўБ¬ПЯЈ¬ИзНјЈє
ГиµгЎўБ¬ПЯЈ¬ИзНјЈє
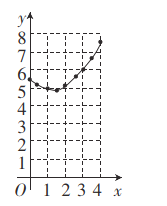
ЈЁ3Ј©УЙЈЁ2Ј©ЦРНјПсїЙЦЄЈє
єЇКэУРЧоРЎЦµЈ¬ТІУРЧоґуЦµЈ»№КўЩґнОуЈ¬ўЪХэИ·Ј»
ЧчµгA№ШУЪBCµД¶ФіЖµгGЈ¬Б¬ЅУDGЈ¬УлBCПаЅ»УЪµгPЈ¬
ФтґЛК±PA+PD=DGОЄЧоРЎЦµЈ»ИзНјЈє
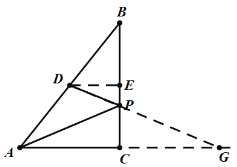
ЎЯDEЎОAGЈ¬
Ўа![]() Ј¬
Ј¬
Ўа Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Ўаµ±![]() К±Ј¬PA+PD=DGУРЧоРЎЦµЈ»
К±Ј¬PA+PD=DGУРЧоРЎЦµЈ»
Ўаµ±![]() К±Ј¬
К±Ј¬![]() ЛжЧЕ
ЛжЧЕ![]() µДФцґу¶шФцґуЈ¬ўЫХэИ·Ј»
µДФцґу¶шФцґуЈ¬ўЫХэИ·Ј»
Ўаµ±![]() К±Ј¬
К±Ј¬![]() ЛжЧЕ
ЛжЧЕ![]() µДФцґу¶шјхРЎЈ¬№КўЬґнОуЈ»
µДФцґу¶шјхРЎЈ¬№КўЬґнОуЈ»
№Кґр°ёОЄЈєўЪўЫЈ®

 ЅМС§Б·РВН¬ІЅБ·П°ПµБРґр°ё
ЅМС§Б·РВН¬ІЅБ·П°ПµБРґр°ё їОЗ°їОєуН¬ІЅБ·П°ПµБРґр°ё
їОЗ°їОєуН¬ІЅБ·П°ПµБРґр°ё їОМГРЎЧчТµПµБРґр°ё
їОМГРЎЧчТµПµБРґр°ё »ЖёФРЎЧґФЄїЪЛгЛЩЛгБ·П°ІбПµБРґр°ё
»ЖёФРЎЧґФЄїЪЛгЛЩЛгБ·П°ІбПµБРґр°ёЎѕМвДїЎїДіРЈЖЯЎў°ЛДкј¶ёчУР300ГыС§ЙъЈ¬ЅьЖЪ¶ФЛыГЗЎ°2020ДкРВРН№ЪЧґІЎ¶ѕЎ±·АЦОЦЄК¶ЅшРРБЛПЯЙПІвКФЈ¬ОЄБЛБЛЅвЛыГЗµДХЖОХЗйїцЈ¬ґУЖЯЎў°ЛДкј¶ёчЛж»ъійИЎБЛ50ГыС§ЙъµДіЙјЁЈЁ°Щ·ЦЦЖЈ©Ј¬Іў¶ФКэѕЭЈЁіЙјЁЈ©ЅшРРХыАнЎўГиКцєН·ЦОцЈ®ПВГжёшіцБЛІї·ЦРЕПўЈє
aЈ®ЖЯДкј¶µДЖµКэ·ЦІјЦ±·ЅНјИзПВЈЁКэѕЭ·ЦОЄ5ЧйЈє50ЎЬxЈј60Ј¬60ЎЬxЈј70Ј¬70ЎЬxЈј80Ј¬80ЎЬxЈј90Ј¬90ЎЬxЎЬ100Ј©Јє

bЈ®ЖЯДкј¶С§ЙъіЙјЁФЪ80ЎЬxЈј90µДХвТ»ЧйКЗЈє
80 80.5 81 82 82 83 83.5 84
84 85 86 86.5 87 88 89 89
cЈ®ЖЯЎў°ЛДкј¶С§ЙъіЙјЁµДЖЅѕщКэЎўЦРО»КэЎўЦЪКэИзПВЈє
Дкј¶ | ЖЅѕщКэ | ЦРО»Кэ | ЦЪКэ |
ЖЯДкј¶ | 85.3 | m | 90 |
°ЛДкј¶ | 87.2 | 85 | 91 |
ёщѕЭТФЙПРЕПўЈ¬»ШґрПВБРОКМвЈє
ЈЁ1Ј©±нЦРmµДЦµОЄ Ј»
ЈЁ2Ј©ФЪЛж»ъійСщµДС§ЙъЦРЈ¬·АЦОЦЄК¶іЙјЁОЄ84·ЦµДС§ЙъЈ¬ФЪ Дкј¶ЕЕГыёьїїЗ°Ј¬АнУЙКЗ Ј»
ЈЁ3Ј©ИфёчДкј¶·АЦОЦЄК¶µДЗ°90ГыЅ«ІОјУПЯЙП·АЦОЦЄК¶ѕєИьЈ¬Ф¤№АЖЯДкј¶·ЦКэЦБЙЩґпµЅ ·ЦµДС§ЙъІЕДЬИлСЎЈ»
ЈЁ4Ј©Иф85·Цј°ТФЙПОЄЎ°УЕРгЎ±Ј¬Зл№АјЖЖЯДкј¶ґпµЅЎ°УЕРгЎ±µДИЛКэЈ®