Question

【题目】已知∠AOB.求作：∠AOB的平分线.(要求：尺规作图，保留作图痕迹，不必写作法)，这种尺规作图得到角平分线的依据是______.

Answer 1

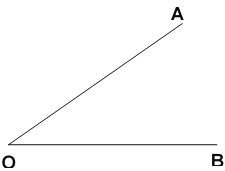
【答案】作图见解析；三条边对应相等的两个三角形全等，全等三角形对应角相等.

【解析】

①以点O为圆心，以适当长为半径作弧交OA、OB于C、D；②分别以点C、D为圆心，以大于CD长为半径作弧，两弧相交于点E；③作射线OE，OE即是∠AOB的平分线；连结CE，DE，根据SSS可证△OCE≌△ODE，可得∠COE=∠DOE，问题得解.

解：如图，射线OE即为所求：

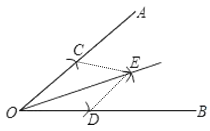
连结CE，DE，

由作图可知：OC=OD，CE=DE，

∵OE=OE，

∴△OCE≌△ODE（SSS），

∴∠COE=∠DOE，即OE为∠AOB的平分线，

∴这种尺规作图得到角平分线的依据是：三条边对应相等的两个三角形全等，全等三角形对应角相等.