题目内容
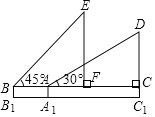
【题目】如图，计划围一个面积为50 m2的长方形场地，一边靠旧墙(墙长为10 m)，另外三边用篱笆围成，并且它的长与宽之比为5∶2.讨论方案时，小英说：“我们不可能围成满足要求的长方形场地．”小军说：“面积和长宽比例是确定的，肯定可以围得出来．”请你判断谁的说法正确，为什么？
【答案】他们的说法都不正确，理由见解析.
【解析】
根据矩形的面积公式求出矩形的长和宽，最后进行判断即可得出结论．
解：设长方形场地的长为5x m，宽为2x m．依题意，得
5x·2x＝50.
∴x＝
.
∴长为5 m，宽为2 m.
∵4＜5＜9，
∴2＜＜3.
由上可知2＜6，且5＞10.
若长与墙平行，墙长只有10 m，故不能围成满足条件的长方形场地；
若宽与墙平行，则能围成满足条件的长方形场地．
∴他们的说法都不正确．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
【题目】随着手机的普及，微信（一种聊天软件）的兴起，许多人抓住这种机会，做起了“微商”很多农产品也改变了原来的销售模式，实行了网上销售，刚大学毕业的小明把自家的冬枣产品也放到了网上，他原计划每天卖
斤冬枣，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某周的销售情况（超额记为正，不足记为负单位：斤）；
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
（1）根据记录的数据可知前三天共卖出 斤；
（2）根据记录的数据可知该周销售量最多的一天比销售量最少的一天多销售 斤；
（3）本周实际销售总量是否达到了计划数量？试通过计算说明理由．
（4）若冬枣每斤按
元出售，每斤冬枣的运费平均
元（运费由小明承担），那么小明本周一共收入多少元？
