题目内容
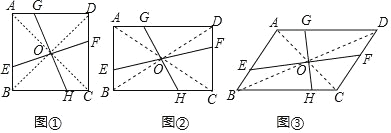
【题目】已知:直线l1与直线l2平行,且它们之间的距离为3,A,B是直线l1上的两个定点,C,D是直线l2上的两个动点(点C在点D的左侧),AB=CD=6,连接AC、BD、BC,将△ABC沿BC折叠得到△A1BC.(如图1)
(1)当A1与D重合时(如图2),四边形ABDC是什么特殊四边形,为什么?
(2)当A1与D不重合时,连接A1D,则A1 D∥BC(不需证明),此时若以A1,B,C,D为顶点的四边形为矩形,且矩形的边长分别为a,b,求(a+b)2的值.
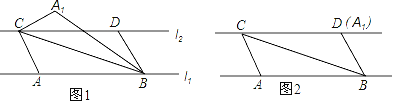
【答案】(1)四边形ABDC是菱形,证明见解析;(2)(a+b)2的值为72或81.
【解析】(1)根据折叠的性质得到AC=CD,然后根据菱形的判定方法可判断四边形ABDC是菱形;
(2)讨论:当∠CBD=90°,则∠BCA=90°,由于S△A1CB=S△ABC=6,则S矩形A1CBD=12,即ab=12,由BA1=BA=6,根据勾股定理得到a2+b2=36,然后根据完全平方公式进行计算;当∠BCD=90°,则∠CBA=90°,易得BC=3,而CD=6,所以(a+b)2=(3+6)2..
(1)四边形ABDC是菱形;
∵AB=CD,AB∥CD,
∴四边形ABCD为平行四边形,
又∵A1与D重合时,
∴AC=CD,
∴四边形ABDC是菱形;
(2)当以A1,B,C,D为顶点的四边形为矩形如图1时,连结A1B,S△A1CB=S△ABC=![]() ×6×3=9
×6×3=9
∴S矩形A1CBD=18,即ab=18,而在Rt△BCD中,
∴a2+b2=CD2=36
∴(a+b)2=a2+b2+2ab=36+36=72,
当以A1,B,C,D为顶点的四边形为矩形如图2时,
∴(a+b)2=(3+6)2=81,
∴(a+b)2的值为72或81.


练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目