��Ŀ����
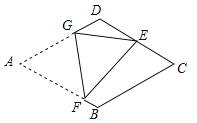
����Ŀ����ͼ��![]() �У�
��![]() ����
����![]() Ϊ����ԭ�㽨��ֱ�Ǽ��ϵ��ʹ��
Ϊ����ԭ�㽨��ֱ�Ǽ��ϵ��ʹ��![]() ��
��![]() ���������ϣ�
���������ϣ�![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() �ߵ��е㣬�����ߵĶ�����ԭ��
�ߵ��е㣬�����ߵĶ�����ԭ��![]() ���Ҿ���
���Ҿ���![]() ��
��
(1)��գ�ֱ��![]() �Ľ���ʽΪ �������ߵĽ���ʽΪ ��
�Ľ���ʽΪ �������ߵĽ���ʽΪ ��
(2)�ֽ��������������߶�![]() �ƶ���ʹ�䶥��
�ƶ���ʹ�䶥��![]() ʼ�����߶�
ʼ�����߶�![]() ��(������
��(������![]() ��
��![]() )����������
)����������![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ����
����![]() �ߵĽ���Ϊ
�ߵĽ���Ϊ![]() ��
��
����![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���Ƿ���������ĵ�![]() ��ʹ�ı���
��ʹ�ı���![]() Ϊƽ���ı��Σ�����ڣ������ʱ�����ߵĽ���ʽ���粻���ڣ�˵�����ɣ�
Ϊƽ���ı��Σ�����ڣ������ʱ�����ߵĽ���ʽ���粻���ڣ�˵�����ɣ�

���𰸡���1��y=2x��y=x2 ����2����![]() ���ڴ��ڣ�
���ڴ��ڣ�![]()
��������
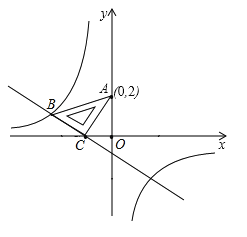
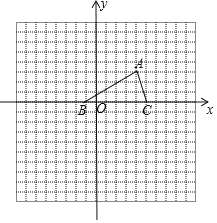
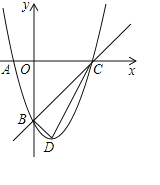
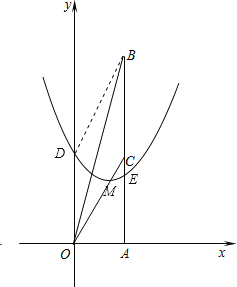
��1���������������C������Ȼ�����ֱ��OC�Ľ���ʽ�������ߵĽ���ʽ��
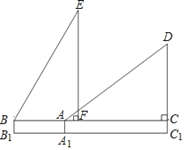
��2���ٸ��������ߵ��ƶ�������������ߵĽ���ʽ�������BOE�����S��m�Ĺ�ϵ���ٸ���m��ȡֵ��Χ�������S��ȡֵ��Χ��
�ڸ���ƽ���ı��ε����ʼ��ɵó�m��ֵ��
�⣺��1����OA=2��AB=8����CΪAB�ߵ��е㣬
���C������Ϊ��2��4���㣬
��ֱ�ߵĽ���ʽΪy=kx
��4=2k�����k=2
��ֱ�ߵĽ���ʽΪy=2x��
�������ߵĽ���ʽΪy=kx2
��4=4k�����k=1
�������ߵĽ���ʽΪy=x2��
��2�����ƶ��������ߵĽ���ʽΪy=��x-m��2+2m��
�� ��![]() ��
��
![]()
![]()
![]()
![]() ��
��
�֡�![]() ��
��
��![]() ��
��
�ڴ��ڵ�D��ʹ�ı���BDOCΪƽ���ı��Σ�
��OD=BC���ı���BDOCΪƽ���ı��Σ�
��OD=BC=![]() =4��
=4��
��ɵ�x=0ʱy=4��
��m2+2m=4��
�ࣨm+1��2=5��
���![]() ��
��![]() ����ȥ����
����ȥ����
����![]() ��
��
��![]()
![]() ��
��

����Ŀ��ijУ��������������������Ϊʦ����֮��Ĺ�ͨ������һ�����潻��������.Ϊ�˽���꼶ѧ������������������ͨ��������ʹ�������ij������Ը�У���꼶ȫ��ѧ��������һ���ʾ����飬�����ݵ����������������в�������ͳ��ͼ.
����������ͨ������������������ʦ�ܹ�Ͷ�ݹ������ţ� |
A.ûͶ�� B.һ�� C.���� D.��������� |
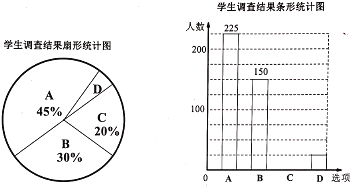
��������ͼ��������������⣺
(1)��У���꼶ѧ������____�ˣ�
(2)ѧ������������ͳ��ͼ�У�����![]() ��Բ�ĽǶ�����______��
��Բ�ĽǶ�����______��
(3)���㲹ȫ����ͳ��ͼ��
(4)���ݵ����������ƶϣ�����������У���꼶ѧ��ͨ��������������Ͷ�ݳ��ż�����������_____��.