题目内容
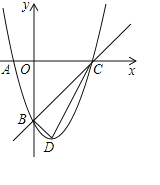
【题目】抛物线y=x2+bx+c的图象经过点A(﹣1,0),B(0,﹣3).
(1)求这个抛物线的解析式;
(2)抛物线与x轴的另一交点为C,抛物线的顶点为D,判断△CBD的形状;
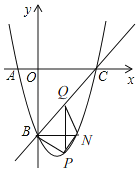
(3)直线BN∥x轴,交抛物线于另一点N,点P是直线BN下方的抛物线上的一个动点(点P不与点B和点N重合),过点P作x轴的垂线,交直线BC于点Q,当四边形BPNQ的面积最大时,求出点P的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)△BCD是直角三角形;(3)P(![]() ,﹣
,﹣![]() )
)
【解析】
(1)根据待定系数法求解即可;
(2)先求出点C、点D的坐标,再进行判断即可;
(3)设P(m,m2﹣2m﹣3)(0<m<2),列式表示S四边形BPNQ,然后根据二次函数的性质求解即可.
解:(1)根据题意得![]() ,
,
解得![]()
∴抛物线的解析式为y=x2﹣2x﹣3;
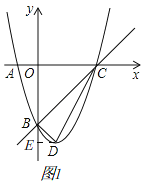
(2)如图1,当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3,
则C(3,0),
∴OC=3,
∵B(0,﹣3),
∴OB=3=OC,
∴∠OBC=45°,
由(1)知,y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的顶点D的坐标为(1,﹣4),
过点D作DE⊥y轴于E,
∴DE=1,OE=4,
∴BE=OE﹣OB=1=DE,
∴∠DBE=45°,
∴∠CBD=180°﹣∠DBE﹣∠OBC=90°,
∴△BCD是直角三角形;
(3)如图,由抛物线的对称性知,N(2,﹣3),
∴BN=2,
∵BN∥x轴,PQ⊥x轴,
∴BN⊥PQ,
设P(m,m2﹣2m﹣3)(0<m<2),
∵B(0,﹣3),C(3,0),
∴直线BC的解析式为y=x﹣3,
∴Q(m,m﹣3),
∴PQ=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m=﹣(m﹣![]() )2+
)2+![]() ,
,
∴S四边形BPNQ=S△PBQ+S△PNQ=![]() PQBN=
PQBN=![]() [﹣(m﹣
[﹣(m﹣![]() )2+
)2+![]() ]×2=﹣(m﹣
]×2=﹣(m﹣![]() )2
)2![]() ,
,
当m=![]() 时,S四边形BPNQ最大,最大值为
时,S四边形BPNQ最大,最大值为![]() ,此时P(
,此时P(![]() ,﹣
,﹣![]() ).
).