Question

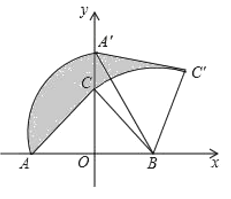
【题目】如图，在平面直角坐标系中，将一块等腰直角三角板放在第二象限，斜靠在两坐标轴上，点坐标为，点的坐标为，一次函数的图象经过点B、C，反比例函数的图象也经过点．

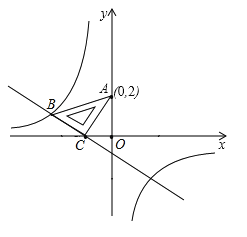
(1)求反比例函数和一次函数的关系式；

(2)观察图象直接写出图象在第二象限时，的解集．

Answer 1

【答案】(1); (2)-3<x<0

【解析】

（1）过点B作BD⊥x轴于点D．根据AAS证明△BCD≌△CAO，从而求得点B的坐标，利用待定系数法可求出反比例函数的关系式；

（2）在第二象限内，找出一次函数值y=kx+b落在反比例函数图象下方的部分对应的x的取值范围即可．

解:(1)过B作BD⊥x轴,垂足为D,

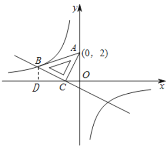
在△BDC和△COA中

∵∠BDC=∠COA=90°

∵∠DCB+∠ACO=∠CAO+∠ACO

∴∠DCB=∠CAO

∵BC=AC,

∴△BDC≌△COA

∴DC=AO=2,BD=CO=1

∴点B的坐标是(-3,1)

将点B(-3,1)代入得

解得m=-3

∴反比例函数的表达式是

将B(-3,1)和点C(-1,0)代入y=kx+b得

∴

解得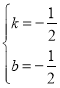

∴一次函数的表达式是

(2)在第二象限内,的解集是-3<x<0