题目内容
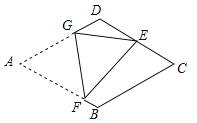
【题目】如图，在菱形ABCD中，AB＝2，∠D＝120°，将菱形翻折，使点A落在边CD的中点E处，折痕交边AD，AB于点G，F，则AF的长为___
【答案】
【解析】
过点E作EH⊥AD于H，EN⊥AB于N，过点A作AM⊥CD于M，根据勾股定理可求AG的长度，可证AMEN为矩形，即NA=ME=2，即B，N重合，再根据勾股定理可求EF的长，由折叠的性质可得解．
过点E作EN⊥AB于N，过点A作AM⊥CD于M，如图
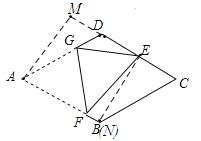
∵ABCD是菱形，
∴AB∥CD，AD=AB=CD=AB=2
∵∠D＝120°，
∴∠ADM=∠BAD=∠HDE=60°，
在Rt△AMD中，AD=2，AM⊥DM，∠ADM=60°
∴MD=1，AM=
，
∵AB∥CD，AM∥EN
∴AMEN是平行四边形且AM⊥CD
∴AMEN是矩形
∴AN=ME=1+1=2，（即N与B重合）
AM=EN=，
在Rt△FBE中，EF2=EN2+FB 2
EF2=（2-EF）2+3
∴EF=.
练习册系列答案
口算题天天练系列答案
相关题目
