题目内容
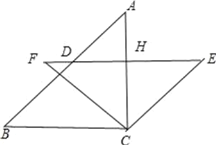
【题目】如图，△ABC中，BC=AC，∠ACB=90°，将△ABC绕着点C顺时针旋转α（0≤α≤90°），得到△EFC，EF与AB、AC相交于点D、H，FC与AB相交于点G、AC相交于点D、H，FC与AB相较于点G．
（1）求证：△GBC≌△HEC；
（2）在旋转过程中，当α是多少度时四边形BCED可以是某种特殊的平行四边形？并说明理由．
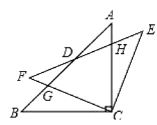
【答案】（1）详见解析；（2）当α=45°时，四边形BCED为菱形，理由详见解析．
【解析】
（1）先判断△ABC为等腰直角三角形得到∠A=∠B=45°，再由旋转的性质得到∠BCF=∠ACE=α，∠E=∠A=45°，CA=CE=CB，最后可根据“ASA”可判断△GBC≌△HEC；
（2）当α=45°时，根据旋转的性质得∠BCF=∠ACE=45°，则可计算出∠BCE=∠BCA+∠ACE=135°，再证BD∥CE，BC∥DE，于是可判断四边形BCED为平行四边形，结合CB=CE，则可判断四边形BCED为菱形．
解：（1）证明：∵BC=AC，∠ACB=90°，
∴△ABC为等腰直角三角形，
∴∠A=∠B=45°，
∵△ABC绕着点C顺时针旋转α°（0≤α≤90°），得到△EFC，
∴∠BCF=∠ACE=α，∠E=∠A=45°，CA=CE=CB，
在△GBC和△HEC中
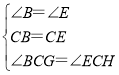
∴△GBC≌△HEC（ASA）；
（2）解：当α=45°时，四边形BCED为菱形．理由如下：
如图，
∵∠BCF=∠ACE=45°，
∴∠BCE=∠BCA+∠ACE=90°+45°=135°，
而∠E=∠B=45°，
∴∠B+∠BCE=180°，∠E+∠BCE=180°，
∴BD∥CE，BC∥DE（同旁内角互补，两直线平行），
∴四边形BCED为平行四边形，
∵CB=CE，
∴四边形BCED为菱形．
练习册系列答案
相关题目
