Question

【题目】阅读下面的材料：

如果函数满足：对于自变量的取值范围内的任意，，

（1）若，都有，则称是增函数；

（2）若，都有，则称是减函数．

例题：证明函数是减函数．

证明：设，

．

∵，∴，．∴．即．

∴．∴函数（）是减函数．

根据以上材料，解答下面的问题：

己知函数（），

（1）计算：_______，_______；

（2）猜想：函数（）是_______函数（填“增”或“减”）；

（3）请仿照例题证明你的猜想．

Answer 1

【答案】（1），；（2）增；（3）证明见解析

【解析】

（1）根据题目中的函数解析式可以解答本题；

（2）由（1）答案可得结论；

（3）根据题目中例子的证明方法可以证明（2）中的猜想成立．

（1）

（2）增函数

（3）=

∵，∴，．

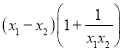
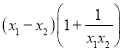∴＜0．即．

∴

∴函数（）是增函数．