Question

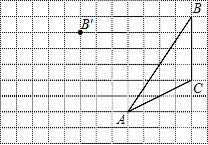
【题目】画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．利用网格点和三角板画图或计算：

（1）在给定方格纸中画出平移后的△A′B′C′；

（2）画出AB边上的中线CD；

（3）画出BC边上的高线AE；

（4）△A′B′C′的面积为 ．

Answer 1

【答案】见解析

【解析】

（1）连接BB′，过A、C分别做BB′的平行线，并且在平行线上截取AA′=CC′=BB′，顺次连接平移后各点，得到的三角形即为平移后的三角形；
（2）作AB的垂直平分线找到中点D，连接CD，CD就是所求的中线．
（3）从A点向BC的延长线作垂线，垂足为点E，AE即为BC边上的高；
（4）根据三角形面积公式即可求出△A′B′C′的面积．

(1)如图所示：△A′B′C′即为所求;

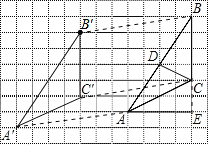
(2)如图所示：CD就是所求的中线；

(3)如图所示：AE即为BC边上的高；

(4)

故△A′B′C′的面积为8.

故答案为：8.