Question

【题目】5月份,某品牌衬衣正式上市销售.5月1日的销售量为10件,5月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到5月31日销售量为零.设该品牌衬衣的日销量为p(件),销售日期为n(日),p与n之间的关系如图所示.

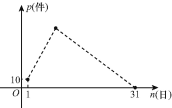
(1)写出p关于n的函数关系式　 　.(注明n的取值范围)

(2)经研究表明,该品牌衬衣的日销量超过150件的时间为该品牌衬衣的流行期.请问:该品牌衬衣本月在市面的流行期是多少天?

Answer 1

【答案】(1) p=(2) 该品牌衬衣本月在市面的流行期为14天.

【解析】

（1）如果设5月x日是最后一天销售量增加的日期，那么根据这一天的销售量不变列出方程，即可求解；

（2）分1≤n≤12时和12＜n≤31两种情况列出不等式，分别求出n的取值范围，然后相加即可．

（1）设5月x日是最后一天销售量增加的日期，

根据题意，有10+25（x-1）=15（31-x），

解得 x=12，

因此，当1≤n≤12且n为整数时，p=10+25（n-1）；

当12＜n≤31且n为整数时，p=15（31-n），

故 p=；

（2）由题意，得

解得6<n<21，

整数n的值可取7，8，9，…，20共14个.

∴该品牌衬衣本月在市面的流行期为14天.