题目内容
【题目】小华将一条直角边长为1的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形(如图3),则图3中的等腰直角三角形的一条腰长为;同上操作,若小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形(如图n+1)的一条腰长为 . 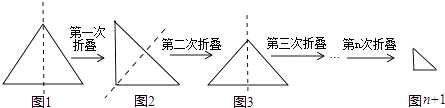
【答案】![]() ;(
;( ![]() )n
)n
【解析】解:每次折叠后,腰长为原来的 ![]() ;
;
故第2次折叠后得到的等腰直角三角形的一条腰长为( ![]() )2=
)2= ![]() ;
;
小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形的一条腰长为( ![]() )n.
)n.
所以答案是: ![]() ;(
;( ![]() )n.
)n.
【考点精析】关于本题考查的翻折变换(折叠问题),需要了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.

练习册系列答案
相关题目
【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对她所任教的初三(1)班和(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况: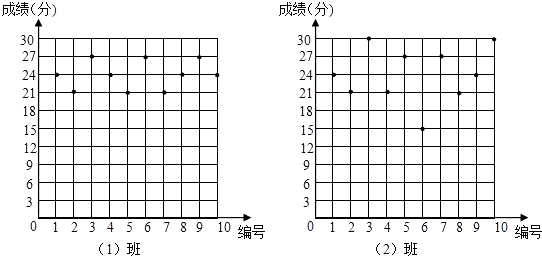
(1)利用图中提供的信息,补全下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
(1)班 | 24 | 24 | |
(2)班 | 24 |
(2)若把24分以上(含24分)记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀;
(3)观察图中的数据分布情况,你认为哪个班的学生纠错的整体情况更好一些?