题目内容
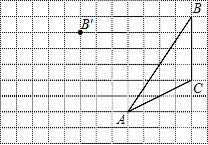
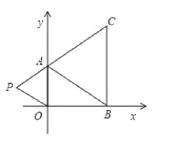
【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a.b.c满足关系式![]() ,c是64的算术平方根.
,c是64的算术平方根.
(1)直接写出a,b,c的值:a=____,b=____,c= ____;
(2)如果在第二象限内有一点P(m,2),请用含m的式子表示四边形APOB的面积S![]() ;
;
(3)在(2)的条件下,是否存在点P,使四边形APOB的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1) a=4, b=6, c=8;(2) 12-2m;(3)存在,理由见解析
【解析】
(1)解方程组即可求出a,b的值,根据c是64的算术平方根即可得出c的值.
(2)根据四边形APOB的面积=△ABO的面积+△APO的面积计算即可;
(3)根据四边形ABOP的面积与△ABC的面积相等,列式可得m=﹣6,从而得P的坐标.
(1)解:∵![]()
∴![]()
∵c是64的算术平方根
∴c=8
故答案为:a=4, b=6, c=8;
(2) 由 (1) 可知: A (0, 4) , B (6, 0) ,C (6,8)
![]() S
S![]() =S
=S![]() +S
+S![]() =
=![]()
![]() 6
6![]() 4+
4+![]()
![]() 4
4![]() |m|=12-2m
|m|=12-2m
(3) 存在
S![]() =
=![]()
![]() BC
BC![]() |x
|x![]() |=
|=![]()
![]() 8
8![]() 6=24
6=24
![]() S
S![]() =24
=24
即:12-2m=24
![]() m=-6
m=-6
![]() 存在P(-6,2),使四边形APOB的面积等于△ABC的面积
存在P(-6,2),使四边形APOB的面积等于△ABC的面积

【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对她所任教的初三(1)班和(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况: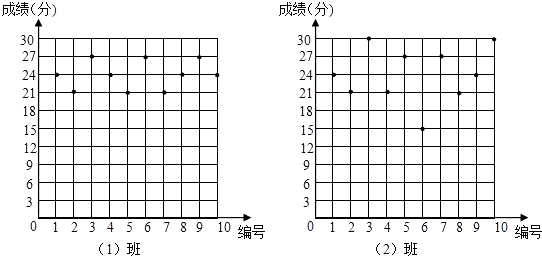
(1)利用图中提供的信息,补全下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
(1)班 | 24 | 24 | |
(2)班 | 24 |
(2)若把24分以上(含24分)记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀;
(3)观察图中的数据分布情况,你认为哪个班的学生纠错的整体情况更好一些?