题目内容
【题目】如图，一艘渔船位于码头M的南偏东45°方向，距离码头120海里的B处，渔船从B处沿正北方向航行一段距离后，到达位于码头北偏东60°方向的A处．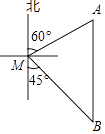
（1）求渔船从B到A的航行过程中与码头M之间的最小距离．
（2）若渔船以20海里/小时的速度从A沿AM方向行驶，求渔船从A到达码头M的航行时间．
【答案】
（1）解：作AC⊥AB于C，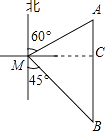 
则MC=BM×cos45°=60 
海里，
答：渔船从B到A的航行过程中与码头M之间的最小距离为60 海里
（2）解：在Rt△ACM中，AM= 
=40 
，
40 ÷20=2 ，
答：渔船从A到达码头M的航行时间为2 小时．
【解析】（1）作AC⊥AB于C， 在Rt△MBC中利用余弦定义得出MC=BM×cos45°即可；（2）在Rt△ACM中，利用利用余弦定义得出AM的长度，再用AM的长度除以渔船的航行速度即可。
【考点精析】认真审题，首先需要了解关于方向角问题(指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角)．
练习册系列答案
相关题目
