题目内容
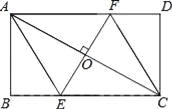
【题目】如图，在矩形ABCD中，AB＝4，BC＝3，BD为对角线．点P从点B出发，沿线段BA向点A运动，点Q从点D出发，沿线段DB向点B运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到A时，两点都停止．设运动时间为t秒．
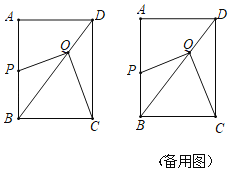
（1）是否存在某一时刻t，使得PQ∥AD？若存在，求出t的值；若不存在，说明理由．
（2）设四边形BPQC的面积为S，求S与t之间的函数关系式．
（3）是否存在某一时刻t，使得S四边形BPQC：S矩形ABCD＝9：20？若存在，求出t的值；若不存在，则说明理由．
（4）是否存在某一时刻t，使得PQ⊥CQ？若存在，求出t的值；若不存在，则说明理由．
【答案】(1) 
；(2) S＝﹣
t2+t+6 ;(3) 满足条件的t的值为2;(4) 
【解析】
（1）利用平行线分线段成比例定理构建方程即可解决问题．
（2）如图1中，作QE⊥AB于E，QF⊥BC于F，利用平行线分线段成比例定理构建方程求出QE，QF即可解决问题；
（3）根据S四边形BPQC：S矩形ABCD＝9：20，构建方程解决问题即可；
（4）如图1中，作QE⊥AB于E，QF⊥BC于F．当PQ⊥QC时，△QEP∽△QFC，则
，由此构建方程即可解决问题．
解：（1）∵四边形ABCD是矩形，
∴∠A＝90°，
∵AB＝4，AD＝BC＝3，
∴BD＝
＝
＝5，
由题意BP＝t，DQ＝t，
∵PQ∥AD，
∴
＝
，
∴
＝
，
∴t＝，
∴满足条件的t的值为；
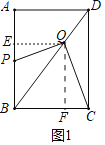
（2）如图1中，作QE⊥AB于E，QF⊥BC于F．
∵QE∥AD，
∴
＝
，
∴
＝，
∴QE＝
（5﹣t），
∵QF∥CD，
∴
＝，
∴
＝，
∴QF＝
（5﹣t），
∴S＝S△PBQ+S△BCQ＝
PBQE+BCQF＝t（5﹣t）+×3×（5﹣t）＝﹣t2+t+6；
（3）由题意：（﹣t2+t+6）：12＝9：20，整理得：t2﹣t﹣2＝0，
解得t＝2或﹣1（舍弃），
∴满足条件的t的值为2；
（4）如图1中，作QE⊥AB于E，QF⊥BC于F．
当PQ⊥QC时，
∵∠EQF＝∠PQC＝90°，
∴∠EQP＝∠FQC，
又∵∠QEP＝∠QFC＝90°，
∴△QEP∽△QFC，
∴，
∴
＝
，
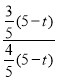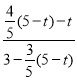解得：t＝，
∴满足条件的t的值为．
