题目内容
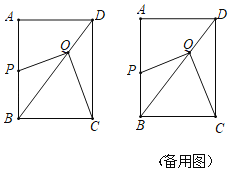
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )

A.4B.3C.2D.1
【答案】B
【解析】
连接PC,根据∠A=30°,BC=2,可知AB的值,根据旋转的性质可知A′B′=AB,进而可知A′P、PB′、PC的知,结合图形和三角形三边关系即可得出PM的取值范围,进而可知P、C、M共线时,PM值最大,即可选出答案.

解:如图连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4,
根据旋转不变性可知,A′B′=AB=4,
∴A′P=PB′,
∴PC=![]() A′B′=2,
A′B′=2,
∵CM=BM=1,
又∵PM≤PC+CM,即PM≤3,
∴PM的最大值为3(此时P、C、M共线).
故选:B.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
【题目】某校为了对甲,乙两名同学进行学生会主席的竞选考核、召开了一次竞选答辩及民主测评会.由A,B,C,D,E五位教师评委对竞选答辩进行评分,并选出20名学生代表参加民主投票.竞选答辩的结果如下表所示:
评委 得分 选手 | A | B | C | D | E |
甲 | 92 | 88 | 90 | 94 | 96 |
乙 | 84 | 86 | 90 | 93 | 91 |

民主投票的结果为:甲8票,乙12票.
根据以上信息解答下列问题:
(1)甲,乙两人的竞选答辩得分分别是多少?
(2)如果综合得分=竞选答辩得分+民主投票得分,那么,甲,乙两人谁当选学生会主席?
(3)如果综合得分=竞选答辩得分![]() 民主投票得分
民主投票得分![]() ,那么,当
,那么,当![]() 时,甲,乙两人谁当选学生会主席?
时,甲,乙两人谁当选学生会主席?