Question

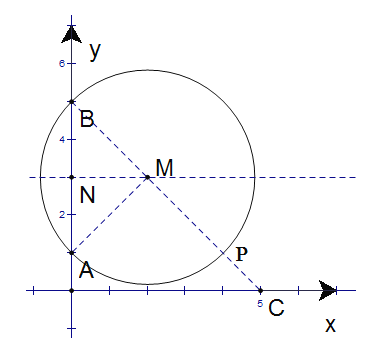
【题目】已知，在平面直角坐标系中，点A（0,1），B(0,5)，C(5,0),且点P在第一象限运动，且∠APB=45°，则PC的最小值为_____.

Answer 1

【答案】.

【解析】

作线段AB的垂直平分线MN交AB于点N，在MN上截取MN＝2,以M为圆心，BM半径作圆，点 , 由MN⊥AB,MN＝AN＝BN，可得∠AMB＝90°,从而可证明点P在优弧上，连接BM并延长交于点P，必交轴于点C,利用勾股定理可得，，答案即可解得.

作线段AB的垂直平分线MN交AB于点N，在MN上截取MN＝2,以M为圆心，BM半径作圆，点 ,

∵MN⊥AB,MN＝AN＝BN,

∴∠MAB＝∠MBA＝45°,

∴∠AMB＝90°,

∴点P在优弧上，∠APB＝45°,

连接BM并延长交于点P，必交轴于点C,

∵BN＝MN＝2,

∴,

∴BP＝,

∵OB＝OC＝5,

∴,

∴PC＝BC－BP＝－＝.