Question

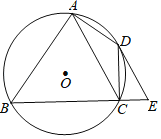
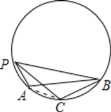
【题目】如图，点是圆上一动点，弦，是的平分线，.

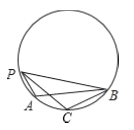
（1）当等于多少度时，四边形有最大面积？最大面积是多少？

（2）当的长为多少时，四边形是梯形？说明你的理由.

Answer 1

【答案】（1）当时，四边形的面积最大，面积为；（2）当或2 时，四边形为梯形.

【解析】

（1）先求得AC=BC，再根据已知条件得S四边形PACB=S△ABC+S△PABS△ABC，当S△PAB最大时，四边形PACB面积最大，求出PC=2，从而计算出最大面积；

（2）已知四边形PACB为梯形，分两种情况：AC∥PB或PA∥BC，求出PA的长．

（1）∵PC平分∠APB，

∴∠APC=∠BPC，

∴AC=BC

由AB＝cm，∠BAC＝30°，求得AC=BC=1cm，

∵S四边形PACB=S△ABC+S△PAB，

S△ABC为定值，

当S△PAB最大时，四边形PACB面积最大，

在△PAB中，AB边不变，其最长的高为过圆心O与AB垂直（即AB的中垂线）与圆O交点P，此时四边形PACB面积最大．易得△PAB为等边三角形，PC为圆的直径，∠PAC=90°，

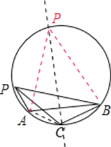
∵∠APC=∠BAC=30°

∴PC=2AC=2，

∴四边形PACB的最大面积为(cm2)；

（2）若四边形PACB为梯形，则当AC∥PB时

由（1）知AC=BC=1，∠CAB=∠PBA=30°，

∴PA=BC=1，

当PA∥BC时，则∠PAB=∠ABC=30°，

在△PBA中，∠APB=60°，

∴∠ABP=180°-60°-30°=90°，

∴此时PA为圆的直径，由（1）知，直径PA=2，

∴当PA=1或2时，四边形PACB为梯形．