题目内容
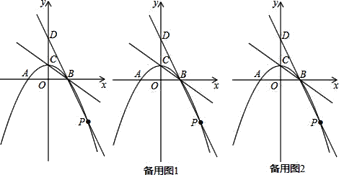
【题目】如图,在平面直角坐标系![]() 中,抛物线与
中,抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),顶点为
的左侧),顶点为![]() .直线
.直线![]() 交
交![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
![]() 求抛物线的表达式及点
求抛物线的表达式及点![]() 的坐标;
的坐标;
![]() 点
点![]() 是抛物线上的动点,若以
是抛物线上的动点,若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形仅有一组对边平行,求点
为顶点的四边形仅有一组对边平行,求点![]() 的坐标;
的坐标;
![]() 连接
连接![]() ,点
,点![]() 在直线
在直线![]() 上,设点
上,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,点
,点![]() 到点
到点![]() 的距离为
的距离为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() 点
点![]() 的坐标为
的坐标为![]() ;(2)点
;(2)点![]() 坐标为
坐标为![]() ,
,![]() ,
,![]() ;(3)12.
;(3)12.
【解析】
(1)设抛物线顶点式解析式y=ax2+1,然后把点P的坐标代入进行计算即可得解;求出抛物线与x轴的交点A、B,然后利用待定系数法求一次函数解析式求出直线DB的解析式,令x=0求出y的值即可得到点D的坐标;
(2)根据四边形仅有一组对边平行,分①AP∥BE,求出直线AP的解析式,再根据平行直线的解析式的k值相等求出直线BE的解析式,与抛物线解析式联立求解即可得到点E的坐标;②AB∥PE,根据抛物线的对称性可得点E与点P关于y轴对称;③BP∥AE,根据平行直线的解析式的k值相等求出AE的解析式,与抛物线解析式联立求解即可得到点E的坐标;
(3)过点P作PM⊥x轴于点M,PN⊥y轴于点N,根据点A、B、P的坐标可以求出∠APM=60°,∠BPM=30°,∠APN=30°,然后求出PA是∠BPN的平分线,过点F作FH⊥PN于点H,连接DF、DH,根据角平分线上的点到角的两边的距离相等可得FH=m,根据三角形的三边关系可得当点D、F、H三点共线时,m+n的值最小,此时,点F为直线AP与y轴的交点,m+n=PN,然后求解即可.
![]() ∵抛物线顶点为
∵抛物线顶点为![]() ,
,
∴设抛物线的解析式是![]() ,
,
又∵点![]() 在抛物线上,
在抛物线上,
∴![]() ,
,
解得![]() ,
,
∴抛物线的解析式为![]() ;
;
令![]() ,则
,则![]() ,
,
解得![]() ,
,![]() ,
,
∴点![]() ,点
,点![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,
,
解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
令![]() ,则
,则![]() ,
,
所以,点![]() 的坐标为
的坐标为![]() ;
;
![]() ①
①![]() 时,设直线
时,设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,
,
解得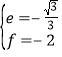 ,
,
所以,直线![]() 的解析式为
的解析式为![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,
,
解得![]() ,
,
所以,直线![]() 的解析式为
的解析式为![]() ,
,
解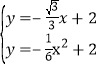 得
得![]() ,
,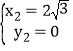 (为点
(为点![]() 的坐标),
的坐标),
所以点![]() 的坐标为
的坐标为![]() ;
;
②![]() 时,∵抛物线关于
时,∵抛物线关于![]() 轴对称,
轴对称,
∴点![]() 为点
为点![]() 关于
关于![]() 轴的对称点,
轴的对称点,
∴点![]() ;
;
③![]() 时,∵直线
时,∵直线![]() 的解析式为
的解析式为![]() ,
,
∴设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,
,
解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
解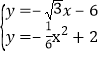 ,得
,得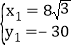 ,
,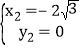 (为点
(为点![]() 坐标),
坐标),
所以,点![]() 坐标为
坐标为![]() ,
,
综上所述,点![]() 坐标为
坐标为![]() ,
,![]() ,
,![]() ;
;
![]() 如图,过点
如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,

∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,根据角平分线的性质可得
,根据角平分线的性质可得![]() ,
,
连接![]() 、
、![]() ,根据三角形的三边关系,
,根据三角形的三边关系,![]() ,
,
即![]() ,
,
所以,当点![]() 、
、![]() 、
、![]() 三点共线时,
三点共线时,![]() 的最小值,
的最小值,
此时,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 、
、![]() 重合,
重合,
最小值![]() .
.