题目内容
【题目】已知抛物线y=﹣x2+![]() x+2与直线y=
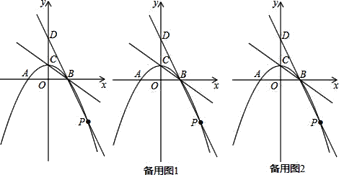
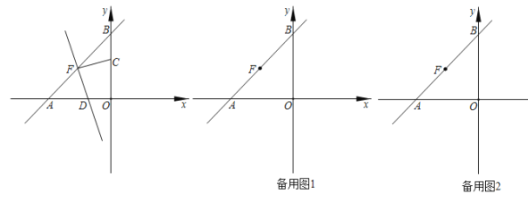
x+2与直线y=![]() x+2相交于点C和D,点P是抛物线在第一象限内的点,它的横坐标为m,过点P作PE⊥x轴,交CD于点F.
x+2相交于点C和D,点P是抛物线在第一象限内的点,它的横坐标为m,过点P作PE⊥x轴,交CD于点F.
(1)求点C和D的坐标;
(2)求抛物线与x轴的交点坐标;
(3)如果以P、C、O、F为顶点的四边形是平行四边形,求m的值.

【答案】(1)C(0,2)和D(3,![]() );(2)(
);(2)(![]() ,0),(4,0);(3)m的值为1、2或
,0),(4,0);(3)m的值为1、2或![]() .
.
【解析】
(1)解抛物线和直线的解析式组成的方程组即可;
(2)令y=0,解一元二次方程即可;
(3)若四边形PCOF是平行四边形,则PF=OC=2,先化简题意表示出点P的坐标为(m,-m2+![]() m+2),点F的坐标为(m,
m+2),点F的坐标为(m,![]() m+2),然后分两种情况讨论求得;
m+2),然后分两种情况讨论求得;
(1)解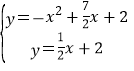 ,则x2+
,则x2+![]() x+2=
x+2=![]() x+2,
x+2,
整理得,x2-3x=0,解得x1=0,x2=3,
∴![]() ,
,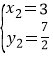 .
.
∴所求的点的坐标是C(0,2)和D(3,![]() );
);
(2)令y=0,则x2+![]() x+2=0,
x+2=0,
解得,x1=![]() ,x2=4,
,x2=4,
∴抛物线与x轴的交点坐标为(![]() ,0),(4,0);
,0),(4,0);
(3)若四边形PCOF是平行四边形,则PF=OC=2,
∵点P的横坐标为m,
∴点P的坐标为(m,-m2+![]() m+2),点F的坐标为(m,
m+2),点F的坐标为(m,![]() m+2),
m+2),
当0<m<3时,PF=(-m2+![]() m+2)-(
m+2)-(![]() m+2),
m+2),
∴-m2+3m=2,m2-3m+2=0,m1=1,m2=2;
当3<m<4时,PF=(![]() m+2)-(-m2+
m+2)-(-m2+![]() m+2),
m+2),
∴m2-3m=2,m2-3m-2=0,m3=![]() ,m4=
,m4=![]() (舍去).
(舍去).
∴如果以P、C、O、F为顶点的四边形是平行四边形,则m的值为1、2或![]() .
.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】一根弹簧的长度为10厘米,当弹簧受到![]() 千克的拉力时(
千克的拉力时(![]() 不超过10),弹簧的长度是
不超过10),弹簧的长度是![]() (厘米),测得有关数据如下表所示:
(厘米),测得有关数据如下表所示:
拉力 | 1 | 2 | 3 | 4 | … |
弹簧的长度 |
|
|
|
| … |
(1)写出弹簧长度![]() (厘米)关于拉力
(厘米)关于拉力![]() (千克)的函数解析式;
(千克)的函数解析式;
(2)如果拉力是10千克,那么弹簧长度是多少厘米?
(3)当拉力是多少时,弹簧长度是14厘米?