Question

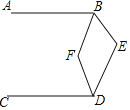
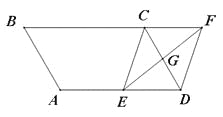
【题目】（7分）如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．

（1）求证：四边形CEDF是平行四边形；

（2）①当AE= cm时，四边形CEDF是矩形；

②当AE= cm时，四边形CEDF是菱形；（直接写出答案，不需要说明理由）

Answer 1

【答案】（1）证明见解析；

（2）① 当AE＝3．5cm时，四边形CEDF是矩形．

② 当AE＝2cm时，四边形CEDF是菱形．

【解析】

试题（1）利用“ASA”即可得证；

①当四边形CEDF是矩形时，则有EG=DG=1．5cm，又由已知可得∠ADC＝60°，从而得△EGD为等边三角形，从而得DE=1．5cm，从而得AE=3．5cm；

②．当四边形CEDF是菱形时，则有EF⊥CD，由已知可知∠ADC=60°，从而可得∠DEG＝30°，从而得DE＝2DG＝3，从而得AE＝2．

试题解析：（1）∵ 四边形ABCD是平行四边形， ∴ CF∥ED， ∴ ∠FCG＝∠EDG，∵ G是CD的中点，∴ CG＝DG，在△FCG和△EDG中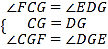，，∴ △FCG ≌△EDG（ASA），∴ FG＝EG，∵ CG＝DG，∴ 四边形CEDF是平行四边形；

（2）① 当AE＝3．5cm时，四边形CEDF是矩形．

② 当AE＝2cm时，四边形CEDF是菱形．