��Ŀ����
����Ŀ����ͼһ,��ƽ��ֱ������ϵ�У�![]() ��
��![]() ����������һ�㣬
����������һ�㣬![]() �ǵ�������һ�㣬
�ǵ�������һ�㣬![]() �ᣬ��
�ᣬ��![]() �Ḻ������
�Ḻ������![]() ����(a-2)+|b+3|=0,
����(a-2)+|b+3|=0,![]() �ı���AOBC=12.
�ı���AOBC=12.
(1)��![]() ������
������
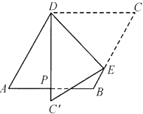
(2)��ͼ��,��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ����(��
��һ����(��![]() �����
�����![]() �غ�)����֤����ADB+��DBC-��OAD=180��
�غ�)����֤����ADB+��DBC-��OAD=180��
(3)��ͼ��,��![]() �����߶�
�����߶�![]() ���˶�(��
���˶�(��![]() �����
�����![]() �غ�)��
�غ�)��![]() �����߶�
�����߶�![]() ���˶�(��
���˶�(��![]() �����
�����![]() �غ�)ʱ������
�غ�)ʱ������![]() ��
��![]() ����OAD����DEB��ƽ���߽���
����OAD����DEB��ƽ���߽���![]() �㣬����̽����AFE����ADE֮��Ĺ�ϵ����˵������.
�㣬����̽����AFE����ADE֮��Ĺ�ϵ����˵������.

���𰸡���1��C��6��-3������2����������� ��3��![]() �����ɼ�����.
�����ɼ�����.
��������
��1�����÷Ǹ����ĺ�Ϊ�㣬����ֱ�Ϊ�㣬���![]() ��
��![]() ���ɣ�
���ɣ�
��2������![]() ��
��![]() �ᣬ����
�ᣬ����![]() ���
���![]() ���ٸ���
���ٸ���![]() ��
��
֪![]() �ᣬ
�ᣬ![]() ���Ӷ�
���Ӷ�![]() ��
��
![]() ������֤��
������֤��![]() ��
��
��3������![]() ��
��![]() �ᣬ����
�ᣬ����![]() ��
��![]() �ᣬ�Ӷ���
�ᣬ�Ӷ���![]() ��
��![]() ����
����![]() ���õ�
���õ�
![]() ����Ϊ
����Ϊ![]() ��
��![]() �Ľ�ƽ���ߺ�
�Ľ�ƽ���ߺ�![]() ��
��![]() �Ľ�ƽ���ߣ�֪
�Ľ�ƽ���ߣ�֪![]() ��
��![]() ����
����![]() ���ٸ���
���ٸ���![]() ���
���![]() ��
��
����![]() ��
��![]() ����
����![]() ����
����
![]() ������
������![]() .
.
��1��![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() �ǵ�������һ�㣬
�ǵ�������һ�㣬![]() ��
��
![]() ��6��-3��
��6��-3��
��2����ͼ��

����![]() ��
��![]() ��
��
![]()
![]()
![]() ��
��
 ��
��
![]()
![]()
![]()
![]()
��3��

![]()
�������£�
����![]() ��
��![]() �ᣬ����
�ᣬ����![]() ��
��![]() ��
��
![]()
![]()
![]() ��
��
![]() ��
��
![]()
![]()
![]()
![]()
![]() ��
��![]() ��ƽ����
��ƽ����
![]()
![]() ��
��![]() �Ľ�ƽ����
�Ľ�ƽ����
![]()
![]()
![]() ��
��
![]()
![]() ��
��
![]() ��
��
![]()
![]()
![]()
![]()
![]()

 ����������ϵ�д�
����������ϵ�д�����Ŀ��Ϊ�˵���ѧ�����������༰Ͷ��֪ʶ���˽�������Ӽס�����У�������ȡ40��ѧ�����������֪ʶ���ԣ���������ǵijɼ����ٷ��ƣ����������ݣ��ɼ��������������������ͷ�������������˲�����Ϣ��
a���ס�����У40��ѧ���ɼ���Ƶ���ֲ�ͳ�Ʊ����£�

��˵�����ɼ�80�ּ�����Ϊ���㣬![]() ��Ϊ���ã�
��Ϊ���ã�![]() ��Ϊ�ϸ�60������Ϊ���ϸ�
��Ϊ�ϸ�60������Ϊ���ϸ�
b����У�ɼ���![]() ��һ����ǣ�70707071727373737475767778
��һ����ǣ�70707071727373737475767778
c���ס�����У�ɼ���ƽ���֡���λ�����������£�
ѧУ | ƽ���֣���λ���֣� | ��λ������λ���֣� | ��������λ���֣� |
�� | 74.2 |
| 85 |
�� | 73.5 | 76 | 84 |
����������Ϣ���ش��������⣺
��1���ϱ���n��ֵΪ_____��
��2���ڴ˴β����У�ijѧ���ijɼ���74�֣���������ѧУ����ǰ20�����ɱ������ݿ�֪��ѧ����___У��ѧ������ס����ҡ�������˵�����ɣ�