ЬтФПФкШн
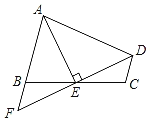
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌABЃНACЃЌЕуDЪЧBCБпЩЯвЛЕуЃЈВЛгыЕуBЃЌCжиКЯЃЉЃЌвдADЮЊБпдкADЕФгвВрзїЁїADEЃЌЪЙADЃНAEЃЌЁЯDAEЃНЁЯBACЃЌСЌНгCEЃЎЩшЁЯBACЃНІСЃЌЁЯBCEЃНІТЃЎ
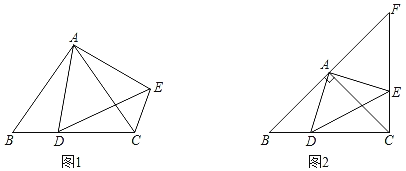
ЃЈ1ЃЉЧѓжЄЃКЁїCAEЁеЁїBADЃЛ
ЃЈ2ЃЉЬНОПЃКЕБЕуDдкBCБпЩЯвЦЖЏЪБЃЌІСЁЂІТжЎМфгадѕбљЕФЪ§СПЙиЯЕЃПЧыЫЕУїРэгЩЃЛ
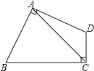
ЃЈ3ЃЉШчЭМ2ЃЌШєЁЯBACЃН90ЁуЃЌCEгыBAЕФбгГЄЯпНЛгкЕуFЃЎЧѓжЄЃКEFЃНDCЃЎ
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉІС+ІТЃН180ЁуЃЛРэгЩМћНтЮіЃЛЃЈ3ЃЉЯъМћНтЮіЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШгЩЁЯDAEЃНЁЯBACЃЌЕУГіЁЯCAEЃНЁЯBADЃЌШЛКѓгЩADЃНAEЃЌACЃНABЃЌМДПЩХаЖЈЁїCAEЁеЁїBADЃЛ
ЃЈ2ЃЉЪзЯШгЩЁїCAEЁеЁїBADЃЌЕУГіЁЯACEЃНЁЯBЃЌШЛКѓгЩABЃНACЃЌЕУГіЁЯBЃНЁЯACBЃЌНјЖјЕУГіЁЯACEЃНЁЯBЃНЁЯACBЃЌЁЯBCEЃНІТЃН2ЁЯBЃЌМДПЩЕУГіІС+ІТЃН180ЁуЃЛ
ЃЈ3ЃЉгЩЁїCAEЁеЁїBADЃЌЕУГіCEЃНBDЃЌдйгЩЁЯBACЃН90ЁуЃЌABЃНACЃЌЕУГіЁЯBЃНЁЯACBЃН45ЁуЃЌгжгЩЁЯBCF+ЁЯBACЃН180ЁуЃЌЕУГіЁЯBCFЃН90ЁуЃЌЁЯFЃНЁЯBЃН45ЁуЃЌНјЖјЕУГіCFЃНCBЃЌМДПЩЕУГіEFЃНDCЃЎ
ЃЈ1ЃЉжЄУїЃКЁпЁЯDAEЃНЁЯBACЃЌ
ЁрЁЯDAEЉЁЯDACЃНЁЯBACЉЁЯDACЃЌ
ЁрЁЯCAEЃНЁЯBADЃЎ
ЁпADЃНAEЃЌACЃНABЃЌ
ЁрЁїCAEЁеЁїBADЃЈSASЃЉЃЎ
ЃЈ2ЃЉНтЃКІС+ІТЃН180ЁуЃЌ
РэгЩШчЯТЃК
гЩЁїCAEЁеЁїBADЃЌ
ЁрЁЯACEЃНЁЯBЃЎ
ЁпABЃНACЃЌ
ЁрЁЯBЃНЁЯACBЃЎ
ЁрЁЯACEЃНЁЯBЃНЁЯACBЃЎ
ЁрЁЯBCEЃНІТЃН2ЁЯBЃЌ
дкЁїABCжаЃЌЁЯBACЃНІСЃН180ЁуЉ2ЁЯBЃЎ
ЁрІС+ІТЃН180ЁуЃЎ
ЃЈ3ЃЉжЄУїЃКгЩЃЈ1ЃЉжЊЃЌЁїCAEЁеЁїBADЃЌ
ЁрCEЃНBDЃЎ
ЁпЁЯBACЃН90ЁуЃЌABЃНACЃЌ
ЁрЁЯBЃНЁЯACBЃН45ЁуЃЌ
гЩЃЈ2ЃЉЕУЃЌЁЯBCF+ЁЯBACЃН180ЁуЃЎ
ЁрЁЯBCFЃН90ЁуЃЎ
ЁрЁЯFЃНЁЯBЃН45ЁуЃЌ
ЁрCFЃНCBЃЎ
ЁрCFЉCEЃНCBЉBDЃЎ
ЁрEFЃНDCЃЎ